题目内容
设函数f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y∈R,有f(x+y)=f(x)·f(y)成立,数列{an}满足a1=f(0)且f(an+1)=(1)求a2 007;
(2)若不等式(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )≥k·
)≥k·![]() 对一切n∈N*均成立,求k的最大值.
对一切n∈N*均成立,求k的最大值.
解:(1)令x=-1,y=0,得f(-1)=f(-1)·f(0)![]() f(0)=1.
f(0)=1.
∴a1=f(0)=1,当x>0时,-x<0,f(-x)>1,f(0)=f(x-x)=f(x)·f(-x)=1.
∴0<f(x)<1.
对任意x1<x2,f(x1)-f(x2)=f(x1)-f(x1+x2-x1)=f(x1)[1-f(x2-x1)]>0,
∴f(x1)>f(x2),∴f(x)为减函数,
由f(an+1)=![]() ,得f(an+1)·f(-2-an)=1,
,得f(an+1)·f(-2-an)=1,
故f(an+1-an-2)=f(0),∴an+1-an-2=0.
因此{an}是首项为1,公差为2的等差数列.
即an+1-an=2(n∈N*),∴a2 007=4 013.an=2n-1.
(2)由(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )≥k·
)≥k·![]() 对一切n∈N*恒成立,
对一切n∈N*恒成立,
知k≤ 恒成立.
恒成立.
设F(n)= 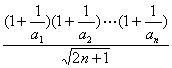 ,则F(n)>0,
,则F(n)>0,
且F(n+1)=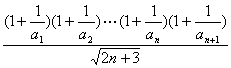 .
.
又![]() >1,
>1,
即F(n+1)>F(n),故F(n)关于n为增函数,
∴F(n)≥F(1)=![]() .∴k≤
.∴k≤![]() ,∴k的最大值为
,∴k的最大值为![]() .
.

练习册系列答案
相关题目