摘要:21. 已知函数上一点P.过点P作直线l. (Ⅰ)求使直线l和y=f(x)相切且以P为切点的直线方程, (Ⅱ)求使直线l和y=f(x)相切且切点异于P的直线方程y=g(x), 的条件下.求上单调时.t的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_4455599[举报]
(本小题满分14分)
已知函数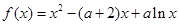 ,其中常数
,其中常数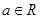 .
.
(Ⅰ)当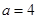 时,求函数
时,求函数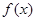 的极值点;
的极值点;
(Ⅱ)令 ,若函数
,若函数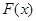 在区间
在区间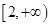 上单调递增,求
上单调递增,求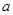 的取值范围;
的取值范围;
(Ⅲ)设定义在D上的函数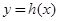 在点
在点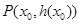 处的切线方程为
处的切线方程为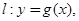 当
当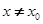 时,若
时,若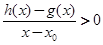 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数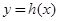 的“特殊点”,请你探究当
的“特殊点”,请你探究当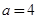 时,函数
时,函数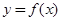 是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
查看习题详情和答案>>
(本小题满分14分)
(1)已知等差数列{an}的前n项和为Sn,若m+n=s+t(m,n,s,t∈N*,且m≠n,s≠t),证明; =
=  ;
;
(2)注意到(1)中Sn与n的函数关系,我们得到命题:设抛物线x2=2py(p>0)的图像上有不同的四点A,B,C,D,若xA,xB,xC,xD分别是这四点的横坐标,且xA+xB=xC+xD,则AB∥CD,判定这个命题的真假,并证明你的结论
(3)我们知道椭圆和抛物线都是圆锥曲线,根据(2)中的结论,对椭圆 +
+ =1(a>b>0)提出一个有深度的结论,并证明之.
=1(a>b>0)提出一个有深度的结论,并证明之.
查看习题详情和答案>>
 ,设
,设 :函数
:函数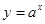 在R上单调递减;
在R上单调递减;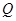 :函数
:函数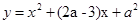 的图象与x轴至少有一个交点.如果P与Q有且只有一个正确,求
的图象与x轴至少有一个交点.如果P与Q有且只有一个正确,求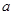 的取值范围.
的取值范围.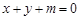 都不与曲线
都不与曲线 相切.
相切. 的取值范围;
的取值范围; 时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于
时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于 .试证明你的结论.
.试证明你的结论. ,其导函数
,其导函数 .
. 试确定b、c的值;
试确定b、c的值; 时,函数
时,函数 的图象上任一点P处的切线斜率为k,若
的图象上任一点P处的切线斜率为k,若 ,求实数b的取值范围。
,求实数b的取值范围。