摘要：22．解:当x＜0时.f(-x)＝()-x-1.而f(x)＝f(-x).f(x)＝)-x-1． 故f(x)＝
网址：http://m.1010jiajiao.com/timu3_id_4455104[举报]
已知f(x)＝x(x－a)(x－b)，点A(s，f(s))，B(t，f(t))．
(1)若a＝b＝1，求函数f(x)的单调递增区间；
(2)若函数f(x)的导函数
满足：当|x|≤1时，有
恒成立，求函数f(x)的解析表达式；
(3)若0＜a＜b，函数f(x)在x＝s和x＝t处取得极值，且a＋b＝
，证明：
与
不可能垂直．
设函数f(x)＝x－a(x＋1)ln(x＋1)，(x＞－1，a≥0)
(Ⅰ)求f(x)的单调区间；
(Ⅱ)当a＝1时，若方程f(x)＝t在[－
，1]上有两个实数解，求实数t的取值范围；
(Ⅲ)证明：当m＞n＞0时，(1＋m)n＜(1＋n)m．
解答题
设f(x)＝x2＋bx＋c(b，c为常数)，方程f(x)－x＝0的两个实根为x1，x2，且满足x1＞0，x2－x1＞1．
(1)求证：b2＞2(b＋2c)；
(2)设0＜t＜x1，比较f(t)与x1的大小；
(3)当x∈[－1，1]时，对任意x都有|f(x)|≤1，
求证：|1＋b|≤2．
查看习题详情和答案>>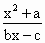
(b，c∈N*)．若方程f(x)＝x有且只有两个相异根0，2，且f(－2)＜－
，
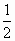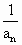)＝1，求数列通项an；
)；②当x＜0时，f(x)＞0
)