题目内容
已知函数f(x)=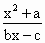 (b,c∈N*).若方程f(x)=x有且只有两个相异根0,2,且f(-2)<-
(b,c∈N*).若方程f(x)=x有且只有两个相异根0,2,且f(-2)<-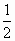 ,
,
(1)求函数f(x)的解析式;
(2)已知各项不为1的数列{an}满足4Sn·f(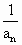 )=1,求数列通项an;
)=1,求数列通项an;
(3)如果数列{an}满足a1=4,an+1=f(an),求证:当n≥2时,恒有an<3成立.
答案:
解析:
解析:
|
解 (1)设 由f(-2)= 又b,c∈N*,∴c=2,b=c,∴f(x)= (2)由已知 相减得(an+an-1)(an-an-1+1)=0, ∴an=-an-1,或an-an-1=-1. 当n=1时,2a1=a1- 这与an≠1矛盾,∴an-an-1=-1,∴an=-n. (3)由an+1=f(an) ∴an+1<0或an+1≥2. 若an+1<0,则an+1<3成立; 若an+1≥2,则an+1-an= ∴{an}在n≥2时单调递减. ∵a2= |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
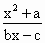 =x
=x (1-b)x2+cx+a=0
(1-b)x2+cx+a=0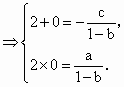

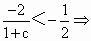 c<3.
c<3. (x≠1).
(x≠1). 2Sn=an-
2Sn=an- ,∴2Sn-1=an-1-
,∴2Sn-1=an-1- .
.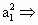 a1=-1.若an=-an-1,则a2=1,
a1=-1.若an=-an-1,则a2=1, an+1=
an+1=
 ≤0.
≤0. ,可知an≤a2=
,可知an≤a2=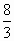 <3在n≥2时成立.
<3在n≥2时成立. )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有