摘要:7.已知O.A.B.C是不共线的四点.若存在一组正实数...使++= .则三个角∠AOB.∠BOC.∠COA ( ) A.都是锐角 B.至多有两个钝角 C.恰有两个钝角 D.至少有两个钝角.
网址:http://m.1010jiajiao.com/timu3_id_4454420[举报]
已知O、A、B、C是不共线的四点,若存在一组正实数λ1﹑λ2﹑λ3,使λ1
+λ2
+λ3
=
,则三个角∠AOB、∠BOC、∠COA( )
| OA |
| OB |
| OC |
| 0 |
| A、都是锐角 |
| B、至多有两个钝角 |
| C、恰有两个钝角 |
| D、至少有两个钝角 |
已知O、A、B、C是不共线的四点,若存在一组正实数λ1﹑λ2﹑λ3,使λ1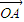 +λ2
+λ2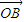 +λ3
+λ3 =
= ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )
A.都是锐角
B.至多有两个钝角
C.恰有两个钝角
D.至少有两个钝角
查看习题详情和答案>>
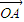 +λ2
+λ2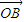 +λ3
+λ3 =
= ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )A.都是锐角
B.至多有两个钝角
C.恰有两个钝角
D.至少有两个钝角
查看习题详情和答案>>
已知O、A、B、C是不共线的四点,若存在一组正实数λ1﹑λ2﹑λ3,使λ1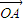 +λ2
+λ2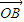 +λ3
+λ3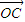 =
=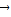 ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )
A.都是锐角
B.至多有两个钝角
C.恰有两个钝角
D.至少有两个钝角
查看习题详情和答案>>
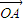 +λ2
+λ2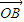 +λ3
+λ3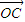 =
=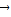 ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )A.都是锐角
B.至多有两个钝角
C.恰有两个钝角
D.至少有两个钝角
查看习题详情和答案>>
已知O、A、B、C是不共线的四点,若存在一组正实数λ1﹑λ2﹑λ3,使λ1 +λ2
+λ2 +λ3
+λ3 =
= ,则三个角∠AOB、∠BOC、∠COA
,则三个角∠AOB、∠BOC、∠COA
- A.都是锐角
- B.至多有两个钝角
- C.恰有两个钝角
- D.至少有两个钝角
 在A,B,C,D四小题中只能选做2题,每题10分,共计20分.
在A,B,C,D四小题中只能选做2题,每题10分,共计20分.A、如图,AB为⊙O的直径,BC切⊙O于B,AC交⊙O于P,CE=BE,E在BC上.求证:PE是⊙O的切线.
B、设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆
| x2 |
| 4 |
| y2 |
| 9 |
C、已知某圆的极坐标方程为:ρ2-4
| 2 |
| π |
| 4 |
(Ⅰ)将极坐标方程化为普通方程;并选择恰当的参数写出它的参数方程;
(Ⅱ)若点P(x,y)在该圆上,求x+y的最大值和最小值.
D、若关于x的不等式|x+2|+|x-1|≥a的解集为R,求实数a的取值范围. 查看习题详情和答案>>