题目内容
已知O、A、B、C是不共线的四点,若存在一组正实数λ1﹑λ2﹑λ3,使λ1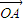 +λ2
+λ2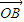 +λ3
+λ3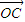 =
=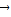 ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )A.都是锐角
B.至多有两个钝角
C.恰有两个钝角
D.至少有两个钝角
【答案】分析:根据λ1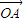 +λ2
+λ2 +λ3
+λ3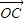 =
= ,移向得λ1
,移向得λ1 +λ2
+λ2 =-λ3
=-λ3 ,两边同时点乘
,两边同时点乘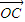 ,得λ1
,得λ1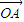 •
• +λ2
+λ2
 =-λ3
=-λ3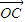
 <0,在根据正实数λ1﹑λ2﹑λ3,和向量数量积的定义即可确定∠BOC、∠COA至少有一个为钝角,同理可证明∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,从而得到结论.
<0,在根据正实数λ1﹑λ2﹑λ3,和向量数量积的定义即可确定∠BOC、∠COA至少有一个为钝角,同理可证明∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,从而得到结论.
解答:解:∵λ1 +λ2
+λ2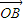 +λ3
+λ3 =
=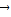 ,
,
∴λ1 +λ2
+λ2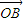 =-λ3
=-λ3 ,两边同时点乘
,两边同时点乘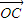 ,得
,得
λ1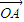 •
•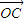 +λ2
+λ2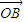
 =-λ3
=-λ3
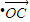 ,
,
即λ1|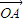 |•|
|•| |cos∠COA+λ2
|cos∠COA+λ2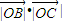 cos∠BOC=-λ3
cos∠BOC=-λ3
 <0,,
<0,,
∴∠BOC、∠COA至少有一个为钝角,
同理∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,
因此∠AOB、∠BOC、∠COA至少有两个钝角.
故选D.
点评:此题是个中档题.考查数量积表示两个向量的夹角,以及数量积的定义式,同时考查学生灵活应用知识分析解决问题的能力和计算能力.
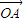 +λ2
+λ2 +λ3
+λ3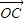 =
= ,移向得λ1
,移向得λ1 +λ2
+λ2 =-λ3
=-λ3 ,两边同时点乘
,两边同时点乘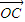 ,得λ1
,得λ1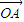 •
• +λ2
+λ2
 =-λ3
=-λ3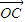
 <0,在根据正实数λ1﹑λ2﹑λ3,和向量数量积的定义即可确定∠BOC、∠COA至少有一个为钝角,同理可证明∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,从而得到结论.
<0,在根据正实数λ1﹑λ2﹑λ3,和向量数量积的定义即可确定∠BOC、∠COA至少有一个为钝角,同理可证明∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,从而得到结论.解答:解:∵λ1
 +λ2
+λ2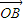 +λ3
+λ3 =
=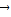 ,
,∴λ1
 +λ2
+λ2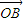 =-λ3
=-λ3 ,两边同时点乘
,两边同时点乘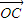 ,得
,得λ1
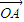 •
•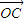 +λ2
+λ2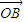
 =-λ3
=-λ3
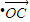 ,
,即λ1|
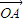 |•|
|•| |cos∠COA+λ2
|cos∠COA+λ2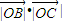 cos∠BOC=-λ3
cos∠BOC=-λ3
 <0,,
<0,,∴∠BOC、∠COA至少有一个为钝角,
同理∠AOB、∠BOC至少有一个为钝角,∠AOB、∠COA至少有一个为钝角,
因此∠AOB、∠BOC、∠COA至少有两个钝角.
故选D.
点评:此题是个中档题.考查数量积表示两个向量的夹角,以及数量积的定义式,同时考查学生灵活应用知识分析解决问题的能力和计算能力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知O、A、B、C是不共线的四点,若存在一组正实数λ1﹑λ2﹑λ3,使λ1
+λ2
+λ3
=
,则三个角∠AOB、∠BOC、∠COA( )
| OA |
| OB |
| OC |
| 0 |
| A、都是锐角 |
| B、至多有两个钝角 |
| C、恰有两个钝角 |
| D、至少有两个钝角 |
 给出下列四个命题:
给出下列四个命题: ;
; ,则α+β=1是A、B、C三点共线的充要条件;
,则α+β=1是A、B、C三点共线的充要条件; (p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
(p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;

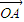 +λ2
+λ2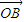 +λ3
+λ3 =
= ,则三个角∠AOB、∠BOC、∠COA( )
,则三个角∠AOB、∠BOC、∠COA( )