摘要: 设甲.乙两人每次射击命中目标的概率分别为.且各次射击相互独立. (Ⅰ)若甲.乙各射击一次.求甲命中但乙未命中目标的概率, (Ⅱ)若甲.乙各射击两次.求两人命中目标的次数相等的概率.
网址:http://m.1010jiajiao.com/timu3_id_4454306[举报]
(本小题满分12分)甲、乙两人射击,每次射击击中目标的概率分别是![]() . 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
. 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
(本小题满分12分)甲、乙两人射击,每次射击击中目标的概率分别是![]() . 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
. 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.(Ⅰ)求3次射击的人依次是甲、甲、乙的概率;(Ⅱ)若射击击中目标一次得1分,否则得0分(含未射击). 用ξ表示乙的总得分,求ξ的分布列和数学期望。
(本小题满分12分)
甲、乙两人各射击一次,击中目标的概率分别是和.假设两人射击是否击中目标相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少有1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中 目标3次的概率.
目标3次的概率.
 和
和 假设两人射击是否击中目标,相互
假设两人射击是否击中目标,相互 表示甲击中目标时射击的次数,求
表示甲击中目标时射击的次数,求 .(结果可以用分数表示)
.(结果可以用分数表示)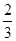 和
和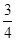 ,假设两人投球是否命中,相互之间没有影响;每次投球是否命中,相互之间也没有影响。
,假设两人投球是否命中,相互之间没有影响;每次投球是否命中,相互之间也没有影响。