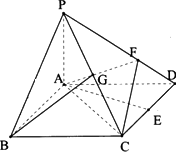
摘要：如图.四棱锥的底面为菱形 且∠ABC＝120°.PA⊥底面ABCD. AB＝2.PA＝. (Ⅰ)求证:平面PBD⊥平面PAC, (Ⅱ)求三棱锥P--BDC的体积. (Ⅲ)在线段PC上是否存在一点E.使PC⊥平面EBD成立．如果存在.求出EC的长,如果不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_4453941[举报]
如图，四棱锥P－ABCD的底面为菱形，且∠ABC－120°，PA⊥底面ABCD，AB＝1，PA＝
，E为PC的中点．
(1)求直线DE与平面PAC所成角的大小；
(2)求二面角E―AD―C的平面角的正切值；
(3)在线段PC上是否存在一点M，使PC⊥平面MBD成立？如果存在，求出MC的长；如果不存在，请说明理由．
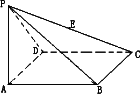
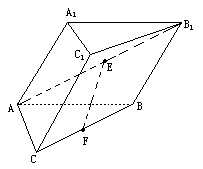
如图，已知斜三棱柱ABC—
的底面是直角三角形，AC⊥CB，∠ABC＝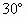
，侧面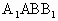
是边长为a的菱形，且垂直于底面，
＝
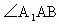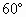，E、F分别是
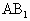、BC的中点．
(Ⅰ)求证：EF∥侧面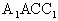
；
(Ⅱ)求四棱锥A—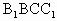
的体积；
(Ⅲ)求EF与侧面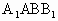
所成角的正切值．
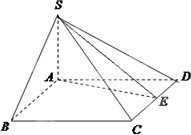
如图，在四棱锥S－ABCD中，SA＝AB＝2，SB＝SD＝2
，底面ABCD是菱形，且∠ABC＝60°，E为CD的中点．
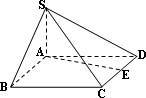
(1)证明：CD⊥平面SAE；
(2)侧棱SB上是否存在点F，使得CF∥平面SAE？并证明你的结论．
，底面ABCD是菱形，且∠ABC＝60°，E为CD的中点．