摘要:5. 曲线 与公共点的个数.
网址:http://m.1010jiajiao.com/timu3_id_4453333[举报]
(1)已知函数f(x)=|x-2|+|x-4|的最小值为m,实数a,b,c,n,p,q
满足a2+b2+c2=n2+p2+q2=m.
(Ⅰ)求m的值; (Ⅱ)求证: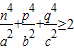 .
.
(2)已知在直角坐标系xOy中,曲线C的参数方程为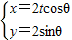 (t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为
(t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为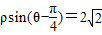 .
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数t,使得直线l与曲线C有两个不同的公共点A、B,且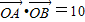 (其中O为坐标原点)?若存在,请求出;否则,请说明理由.
(其中O为坐标原点)?若存在,请求出;否则,请说明理由.
查看习题详情和答案>>
满足a2+b2+c2=n2+p2+q2=m.
(Ⅰ)求m的值; (Ⅱ)求证:
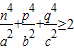 .
.(2)已知在直角坐标系xOy中,曲线C的参数方程为
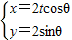 (t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为
(t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为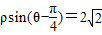 .
.(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数t,使得直线l与曲线C有两个不同的公共点A、B,且
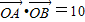 (其中O为坐标原点)?若存在,请求出;否则,请说明理由.
(其中O为坐标原点)?若存在,请求出;否则,请说明理由.查看习题详情和答案>>
选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系xOy的原点,极轴为z轴的正半轴,两种坐标系的长度单位相同,己知圆C1的极坐标方程为p=4(cosθ+sinθ,P是C1上一动点,点Q在射线OP上且满足OQ= OP,点Q的轨迹为C2.
OP,点Q的轨迹为C2.
(I)求曲线C2的极坐标方程,并化为直角坐标方程;
( II)已知直线l的参数方程为 (t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.
(t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.
查看习题详情和答案>>
极坐标系的极点为直角坐标系xOy的原点,极轴为z轴的正半轴,两种坐标系的长度单位相同,己知圆C1的极坐标方程为p=4(cosθ+sinθ,P是C1上一动点,点Q在射线OP上且满足OQ=
 OP,点Q的轨迹为C2.
OP,点Q的轨迹为C2.(I)求曲线C2的极坐标方程,并化为直角坐标方程;
( II)已知直线l的参数方程为
 (t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.
(t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.查看习题详情和答案>>
(2012•唐山二模)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系xOy的原点,极轴为z轴的正半轴,两种坐标系的长度单位相同,己知圆C1的极坐标方程为p=4(cosθ+sinθ,P是C1上一动点,点Q在射线OP上且满足OQ=
OP,点Q的轨迹为C2.
(I)求曲线C2的极坐标方程,并化为直角坐标方程;
( II)已知直线l的参数方程为
(t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.
查看习题详情和答案>>
极坐标系的极点为直角坐标系xOy的原点,极轴为z轴的正半轴,两种坐标系的长度单位相同,己知圆C1的极坐标方程为p=4(cosθ+sinθ,P是C1上一动点,点Q在射线OP上且满足OQ=
| 1 |
| 2 |
(I)求曲线C2的极坐标方程,并化为直角坐标方程;
( II)已知直线l的参数方程为
|
(1)已知函数f(x)=|x-2|+|x-4|的最小值为m,实数a,b,c,n,p,q
满足a2+b2+c2=n2+p2+q2=m.
(Ⅰ)求m的值; (Ⅱ)求证:
+
+
≥2.
(2)已知在直角坐标系xOy中,曲线C的参数方程为
(t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin(θ-
)=2
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数t,使得直线l与曲线C有两个不同的公共点A、B,且
•
=10(其中O为坐标原点)?若存在,请求出;否则,请说明理由.
查看习题详情和答案>>
满足a2+b2+c2=n2+p2+q2=m.
(Ⅰ)求m的值; (Ⅱ)求证:
| n4 |
| a2 |
| p4 |
| b2 |
| q4 |
| c2 |
(2)已知在直角坐标系xOy中,曲线C的参数方程为
|
| π |
| 4 |
| 2 |
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数t,使得直线l与曲线C有两个不同的公共点A、B,且
| OA |
| OB |
(1)已知函数f(x)=|x-2|+|x-4|的最小值为m,实数a,b,c,n,p,q
满足a2+b2+c2=n2+p2+q2=m.
(Ⅰ)求m的值; (Ⅱ)求证:
+
+
≥2.
(2)已知在直角坐标系xOy中,曲线C的参数方程为
(t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin(θ-
)=2
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数t,使得直线l与曲线C有两个不同的公共点A、B,且
•
=10(其中O为坐标原点)?若存在,请求出;否则,请说明理由.
查看习题详情和答案>>
满足a2+b2+c2=n2+p2+q2=m.
(Ⅰ)求m的值; (Ⅱ)求证:
| n4 |
| a2 |
| p4 |
| b2 |
| q4 |
| c2 |
(2)已知在直角坐标系xOy中,曲线C的参数方程为
|
| π |
| 4 |
| 2 |
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数t,使得直线l与曲线C有两个不同的公共点A、B,且
| OA |
| OB |