题目内容
(1)已知函数f(x)=|x-2|+|x-4|的最小值为m,实数a,b,c,n,p,q满足a2+b2+c2=n2+p2+q2=m.
(Ⅰ)求m的值; (Ⅱ)求证:
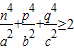 .
.(2)已知在直角坐标系xOy中,曲线C的参数方程为
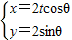 (t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为
(t为非零常数,θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为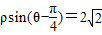 .
.(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数t,使得直线l与曲线C有两个不同的公共点A、B,且
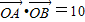 (其中O为坐标原点)?若存在,请求出;否则,请说明理由.
(其中O为坐标原点)?若存在,请求出;否则,请说明理由.
【答案】分析:(1)(Ⅰ)解法一,利用绝对值的几何意义,化简函数,即可求m的值;
解法二:利用绝对值的性质,可得结论;
(Ⅱ)利用柯西不等式,即可证明;
(2)(Ⅰ)消去参数θ,可得普通方程;
(Ⅱ)直线与切线方程联立,利用韦达定理,结合向量知识,可求实数t的值.
解答:(1)(Ⅰ)解法一: ,可得函数的最小值为2.故m=2.
,可得函数的最小值为2.故m=2.
法二:f(x)=|x-2|+|x-4|≥|(x-2)-(x-4)|=2,
当且仅当2≤x≤4时,等号成立,故m=2.
(Ⅱ)证明:∵

∴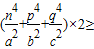 (n2+p2+q2)2=4,故
(n2+p2+q2)2=4,故 .
.
(2)解:(Ⅰ)∵t≠0,∴可将曲线C的方程化为普通方程: .…1分
.…1分
①当t=±1时,曲线C为圆心在原点,半径为2的圆; …2分
②当t≠±1时,曲线C为中心在原点的椭圆.…3分
(Ⅱ)直线l的普通方程为:x-y+4=0.…4分
联立直线与曲线的方程,消y得 ,化简得(1+t2)x2+8t2x+12t2=0.
,化简得(1+t2)x2+8t2x+12t2=0.
若直线l与曲线C有两个不同的公共点,则△=64t4-4(1+t2)•12t2>0,解得t2>3.
又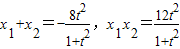 ,…6分
,…6分
故 =2x1x2+4(x1+x2)+16=10.
=2x1x2+4(x1+x2)+16=10.
解得t2=3与t2>3相矛盾.故不存在满足题意的实数t.…7分.
点评:本题考查柯西不等式的运用,考查直线与曲线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.
解法二:利用绝对值的性质,可得结论;
(Ⅱ)利用柯西不等式,即可证明;
(2)(Ⅰ)消去参数θ,可得普通方程;
(Ⅱ)直线与切线方程联立,利用韦达定理,结合向量知识,可求实数t的值.
解答:(1)(Ⅰ)解法一:
 ,可得函数的最小值为2.故m=2.
,可得函数的最小值为2.故m=2.法二:f(x)=|x-2|+|x-4|≥|(x-2)-(x-4)|=2,
当且仅当2≤x≤4时,等号成立,故m=2.
(Ⅱ)证明:∵


∴
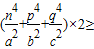 (n2+p2+q2)2=4,故
(n2+p2+q2)2=4,故 .
.(2)解:(Ⅰ)∵t≠0,∴可将曲线C的方程化为普通方程:
 .…1分
.…1分①当t=±1时,曲线C为圆心在原点,半径为2的圆; …2分
②当t≠±1时,曲线C为中心在原点的椭圆.…3分
(Ⅱ)直线l的普通方程为:x-y+4=0.…4分
联立直线与曲线的方程,消y得
 ,化简得(1+t2)x2+8t2x+12t2=0.
,化简得(1+t2)x2+8t2x+12t2=0.若直线l与曲线C有两个不同的公共点,则△=64t4-4(1+t2)•12t2>0,解得t2>3.
又
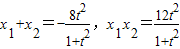 ,…6分
,…6分故
 =2x1x2+4(x1+x2)+16=10.
=2x1x2+4(x1+x2)+16=10.解得t2=3与t2>3相矛盾.故不存在满足题意的实数t.…7分.
点评:本题考查柯西不等式的运用,考查直线与曲线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目