摘要:过圆外一点M引圆x+y=4的两条切线.则经过两切点的直线方程为 A 4x-y-4=0 B4x+y-4=0 C4x+y+4=0 D4x-y+4=0
网址:http://m.1010jiajiao.com/timu3_id_4453124[举报]
过点Q (-2,
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
(1)求r的值;
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设
=
+
,求|
|的最小值(O为坐标原点).
(3)从圆O外一点M(x1,y1)向该圆引一条切线,切点为T,N(2,3),且有|MT|=|MN|,求|MT|的最小值,并求此时点M的坐标.
查看习题详情和答案>>
| 21 |
(1)求r的值;
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设
| OK |
| OA |
| OB |
| OK |
(3)从圆O外一点M(x1,y1)向该圆引一条切线,切点为T,N(2,3),且有|MT|=|MN|,求|MT|的最小值,并求此时点M的坐标.
过点Q(-2,
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
(1)求r的值;
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设
=
+
,求|
|的最小值(O为坐标原点).
(3)从圆O外一点M(x1,y1)向该圆引一条切线,切点为T,N(2,3),且有|MT|=|MN|,求|MT|的最小值,并求此时点M的坐标.
查看习题详情和答案>>
| 21 |
(1)求r的值;
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设
| OK |
| OA |
| OB |
| OK |
(3)从圆O外一点M(x1,y1)向该圆引一条切线,切点为T,N(2,3),且有|MT|=|MN|,求|MT|的最小值,并求此时点M的坐标.
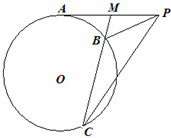
 (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.(2)在平面直角坐标系xOy中,已知四边形ABCD的四个顶点A(0,1),B(2,1),C(2,3),D(0,2),经矩阵M=
|
(3)已知A是曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
| π |
| 6 |
(4)设p是△ABC内的一点,x,y,z是p到三边a,b,c的距离,R是△ABC外接圆的半径,证明
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(2)在平面直角坐标系xOy中,已知四边形ABCD的四个顶点A(0,1),B(2,1),C(2,3),D(0,2),经矩阵M=
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.
(3)已知A是曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
)上的动点,试求AB的最大值.
(4)设p是△ABC内的一点,x,y,z是p到三边a,b,c的距离,R是△ABC外接圆的半径,证明
+
+
≤
.
查看习题详情和答案>>
(2)在平面直角坐标系xOy中,已知四边形ABCD的四个顶点A(0,1),B(2,1),C(2,3),D(0,2),经矩阵M=
|
(3)已知A是曲线ρ=12sinθ上的动点,B是曲线ρ=12cos(θ-
| π |
| 6 |
(4)设p是△ABC内的一点,x,y,z是p到三边a,b,c的距离,R是△ABC外接圆的半径,证明
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |

 表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.
表示的变换作用后,四边形ABCD变为四边形A1B1C1D1,问:四边形ABCD与四边形A1B1C1D1的面积是否相等?试证明你的结论.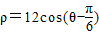 上的动点,试求AB的最大值.
上的动点,试求AB的最大值. .
.