摘要:异于原点O的两点A , B的坐标分别为( x1 , y1 ).( x2 , y2 ). 则“ 是“OA⊥OB 的( ) A.必要条件 B.充分条件 C.充要条件 D.既不充分与不必要条件
网址:http://m.1010jiajiao.com/timu3_id_4452702[举报]
中心在原点,焦点在x轴上,离心率e=
的椭圆的短轴上两端点分别为A、B.M是椭圆上异于A、B的一点,直线AM、BM与x轴分别相交于P、Q两点,O是坐标原点,若
•
=2,求椭圆的方程.
查看习题详情和答案>>
| ||
| 2 |
. |
| OP |
. |
| OQ |
已知A、B分别是椭圆
+
=1的左右两个焦点,O为坐标原点,点P(-1,
)在椭圆上,线段PB与y轴的交点M为线段PB的中点.
(1)求椭圆的标准方程;
(2)点C是椭圆上异于长轴端点的任意一点,对于△ABC,求
的值.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的标准方程;
(2)点C是椭圆上异于长轴端点的任意一点,对于△ABC,求
| sinA+sinB |
| sinC |
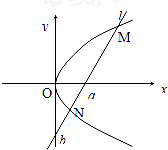 如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b,且交抛物线y2=2px(p>0)于M(x1,y1)、N(x2,y2)两点(异于原点).
如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b,且交抛物线y2=2px(p>0)于M(x1,y1)、N(x2,y2)两点(异于原点).(1)证明:
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| b |
(2)当a=2p时,求证:OM⊥ON.
 的左右两个焦点,O为坐标原点,点P(-1,
的左右两个焦点,O为坐标原点,点P(-1, )在椭圆上,线段PB与y轴的交点M为线段PB的中点.
)在椭圆上,线段PB与y轴的交点M为线段PB的中点.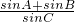 的值.
的值.