题目内容
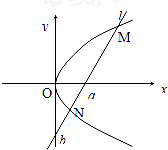如图，O为坐标原点，直线l在x轴和y轴上的截距分别是a和b，且交抛物线y2=2px（p＞0）于M（x1，y1）、N（x2，y2）两点（异于原点）．（1）证明：
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| b |
（2）当a=2p时，求证：OM⊥ON．
分析：（1）写出直线的截距式方程，与抛物线方程联立消去x可得y的二次方程，把等式左侧同分后将韦达定理代入即可证明；
（2）设直线OM、ON的斜率分别为k1、k2，则k1=
，k2=
．代入韦达定理可证明k1k2=-1，从而证明结论；
（2）设直线OM、ON的斜率分别为k1、k2，则k1=
| y1 |
| x1 |
| y2 |
| x2 |
解答：证明：（1）直线的截距式方程为
+
=1与y2=2px联立消去x可得by2+2pay-2pab=0．①
点M、N的纵坐标y1、y2为①的两个根，故y1+y2=-
，y1y2=-2pa．
所以
+
=
=
=
．
（2）设直线OM、ON的斜率分别为k1、k2，
则k1=
，k2=
．
当a=2p时，由（2）知，y1y2=-2pa=-4p2，
由y12=2px1，y22=2px2，相乘得（y1y2）2=4p2x1x2，
x1x2=
=
=4p2，
因此k1k2=
=
=-1．
所以OM⊥ON．
| x |
| a |
| y |
| b |
点M、N的纵坐标y1、y2为①的两个根，故y1+y2=-
| 2pa |
| b |
所以
| 1 |
| y1 |
| 1 |
| y2 |
| y1+y2 |
| y1y2 |
| ||
| -2pa |
| 1 |
| b |
（2）设直线OM、ON的斜率分别为k1、k2，
则k1=
| y1 |
| x1 |
| y2 |
| x2 |
当a=2p时，由（2）知，y1y2=-2pa=-4p2，
由y12=2px1，y22=2px2，相乘得（y1y2）2=4p2x1x2，
x1x2=
| (y1y2)2 |
| 4p2 |
| (4p2)2 |
| 4p2 |
因此k1k2=
| y1y2 |
| x1x2 |
| -4p2 |
| 4p2 |
所以OM⊥ON．
点评：本题考查圆锥曲线的性质和应用，解题时要根据实际情况，注意培养计算能力，把握公式的灵活运用，仔细审题，谨慎作答，避免不必要的错误．
练习册系列答案
相关题目
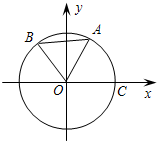如图，O为坐标原点，点A，B，C均在⊙O上，点A
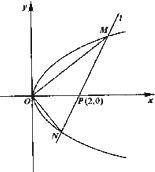如图，O为坐标原点，过点P（2，0）且斜率为k的直线l交抛物线y2=2x于M（x1，y1），N（x2，y2）两点．
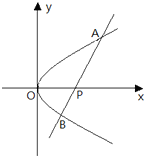（文）如图，O为坐标原点，过点P（2，0）且斜率为k的直线l交抛物线y2=2x于A（x1，y1），B（x2，y2）两点．
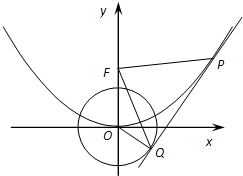如图，O为坐标原点，点F为抛物线C1：x2=2py（p＞0）的焦点，且抛物线C1上点P处的切线与圆C2：x2+y2=1相切于点Q．