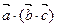摘要:已知=, =.=给出下列等式: ①∣∣=∣∣ ② = ③= ④ = 其中正确的个数是 A.1个 B.2个 C.3个 D.4个
网址:http://m.1010jiajiao.com/timu3_id_4452614[举报]
给出下列3个说法:
①已知甲:x+y=3,已知乙:x=1且y=2,则甲是乙的必要不充分条件
②命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”
③不等式x2-6x+5<0成立的一个充分不必要条件是x>1,
则其中所有正确说法的序号是
查看习题详情和答案>>
①已知甲:x+y=3,已知乙:x=1且y=2,则甲是乙的必要不充分条件
②命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”
③不等式x2-6x+5<0成立的一个充分不必要条件是x>1,
则其中所有正确说法的序号是
①②
①②
.给出下列三个命题:
①命题:“?x∈R,x3-2≤0”的否定为:“?x∈R,x3-2>0”;
②已知甲:x+y=3,乙:x=1且y=2,则甲是乙的必要不充分条件;
③不等式x2-6x+5<0成立的一个充分不必要条件是x<3.
其中真命题的序号是
查看习题详情和答案>>
①命题:“?x∈R,x3-2≤0”的否定为:“?x∈R,x3-2>0”;
②已知甲:x+y=3,乙:x=1且y=2,则甲是乙的必要不充分条件;
③不等式x2-6x+5<0成立的一个充分不必要条件是x<3.
其中真命题的序号是
①②
①②
.(请将所有真命题的序号都填上)16、给出下列命题:
①关于x的的不等式(a-2)x2+(a-2)x+1>0的解集为R的充要条件是2<a<6;
②我们定义非空集合A的真子集的真子集为A的“孙集”,则集合{1,3,5,7,9}的“孙集”有26个.
③已知f(x)=ax2+bx+c(a≠0),若方程f(x)无实数根,则方程f[f(x)]=x也一定没有实数根;
④若{an}成等比数列,Sn是前n项和,则S4,S8-S4,S12-S8成等比数列.
其中正确命题的序号是
查看习题详情和答案>>
①关于x的的不等式(a-2)x2+(a-2)x+1>0的解集为R的充要条件是2<a<6;
②我们定义非空集合A的真子集的真子集为A的“孙集”,则集合{1,3,5,7,9}的“孙集”有26个.
③已知f(x)=ax2+bx+c(a≠0),若方程f(x)无实数根,则方程f[f(x)]=x也一定没有实数根;
④若{an}成等比数列,Sn是前n项和,则S4,S8-S4,S12-S8成等比数列.
其中正确命题的序号是
②③④
.给出下列命题:
(1)函数f(x)=log3(x2-2x)的单调减区间为(-∞,1);
(2)已知P:|2x-3|>1,q:
>0,则p是q的必要不充分条件;
(3)命题“?x∈R,sinx≤
”的否定是:“?x∈R,sinx>”;
(4)已知函数f(x)=
sinωx+cosωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则y=f(x)的单调递增区间是[kπ-
,kπ+
],k∈z;
(5)用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1);
其中所有正确的个数是( )
(1)函数f(x)=log3(x2-2x)的单调减区间为(-∞,1);
(2)已知P:|2x-3|>1,q:
| 1 |
| x2+x-6 |
(3)命题“?x∈R,sinx≤
| 1 |
| 2 |
(4)已知函数f(x)=
| 3 |
| π |
| 3 |
| π |
| 6 |
(5)用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1);
其中所有正确的个数是( )
查看习题详情和答案>>
 =(1,2,3),
=(1,2,3),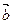 =(3,0,-1),
=(3,0,-1),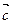 =
=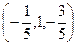 给出下列等式:
给出下列等式: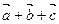 ∣=∣
∣=∣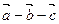 ∣ ②
∣ ②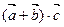 =
=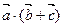 ③
③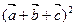 =
=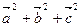
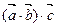 =
=