题目内容
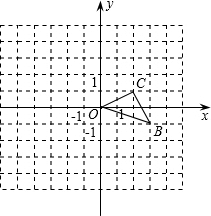 如图已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)
如图已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)(1)画出以O点为旋转中心逆时针旋转90度得到的△B′OC′,并写出B、C两点的对应点B′、C′的坐标;
(2)求点C旋转到点C′所经过的路线长(结果保留π).
分析:(1)根据旋转中心为O、旋转角度为90°,旋转方向为逆时针,找到各点的对应点,顺次连接即可,结合直角坐标系可得出B′、C′的坐标.
(2)点C旋转到点C′所经过的路线长,是以点O为圆心,以OC为半径的扇形的弧长.
(2)点C旋转到点C′所经过的路线长,是以点O为圆心,以OC为半径的扇形的弧长.
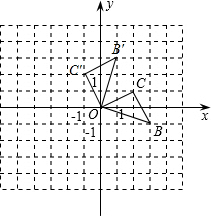
解答:解:(1)所作图形如下:
 .
.
结合直角坐标系可得:B′(1,3),C′(-1,2),
(2)由图形可得:OC=
=
,
故点C旋转到点C′所经过的路线长=
=
=
.
 .
.结合直角坐标系可得:B′(1,3),C′(-1,2),
(2)由图形可得:OC=
| 22+12 |
| 5 |
故点C旋转到点C′所经过的路线长=
| nπR |
| 180 |
| 90°πR |
| 180° |
| ||
| 2 |
点评:本题考查了旋转作图及弧长的计算,作图的关键是根据旋转的性质得到各点的对称点,求路线长关键是利用弧长的计算公式.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
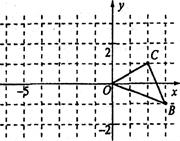
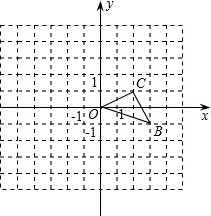 如图已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)
如图已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)