题目内容
已知,在直角坐标系中,△ABO的位置如图1,点O是坐标原点,点A的坐标为(-3,4),AB=AO,AB∥x轴交于y轴于点H.

(1)填空:点B的坐标(
(2)把△ABO沿直线OB翻折得到△CBO,连接AC交于y轴于点M,请在图2 中画出图形,并判断此时四边形AOCB的形状,说明理由.
(3)连接BM,动点P从点A出发,沿折线ABC方向向终点C匀速运动,点P的运动时间为t秒,点P的速度为每秒2个单位,设△PMB的面积为S(S≠0),求当t为何值时,S有最大值,并求出S的最大值.
(4)在(3)条件下,点P在运动过程中,当∠MPB+∠BCO=90°时,求直线OP与直线AC所夹锐角的正切值.

(1)填空:点B的坐标(
2
2
,4
4
),△ABO的面积是10
10
.(2)把△ABO沿直线OB翻折得到△CBO,连接AC交于y轴于点M,请在图2 中画出图形,并判断此时四边形AOCB的形状,说明理由.
(3)连接BM,动点P从点A出发,沿折线ABC方向向终点C匀速运动,点P的运动时间为t秒,点P的速度为每秒2个单位,设△PMB的面积为S(S≠0),求当t为何值时,S有最大值,并求出S的最大值.
(4)在(3)条件下,点P在运动过程中,当∠MPB+∠BCO=90°时,求直线OP与直线AC所夹锐角的正切值.
分析:(1)知道点A的坐标,由条件可以知道点B的横坐标,作AT⊥x轴于点T,由勾股定理可以求出AO的值,从而求出HB就可以求出B点的坐标.
(2)根据轴对称的性质,可以得到OC=OA,BC=AB,再由条件可以得到四边都相等从而得出结论.
(3)根据题意求出C点的坐标,从而求出直线AC的解析式,再求出AC与y轴的交点坐标M,再根据点P在移动过程中的变化情况P在AB和AC上时求出其△PMB的面积解析式,最后求出结论.
(4)根据条件分为两种情况,当P点AB上或P点在BC上证明三角形相似,由相似三角形的性质及菱形的性质求出相应的线段的长度,根据在直角三角形中的三角函数值的计算方法就可以求出两种不同的位置时的直线OP与直线AC所夹锐角的正切值.
(2)根据轴对称的性质,可以得到OC=OA,BC=AB,再由条件可以得到四边都相等从而得出结论.
(3)根据题意求出C点的坐标,从而求出直线AC的解析式,再求出AC与y轴的交点坐标M,再根据点P在移动过程中的变化情况P在AB和AC上时求出其△PMB的面积解析式,最后求出结论.
(4)根据条件分为两种情况,当P点AB上或P点在BC上证明三角形相似,由相似三角形的性质及菱形的性质求出相应的线段的长度,根据在直角三角形中的三角函数值的计算方法就可以求出两种不同的位置时的直线OP与直线AC所夹锐角的正切值.
解答: 解:(1)如图1,作AT⊥x轴于点T,
解:(1)如图1,作AT⊥x轴于点T,
∴∠ATO=90°,
∵A(-3,4),
∴AT=4,TO=3,在Rt△AOT中由勾股定理,得
AO=
=5.
∵AB=AO,
∴AO=5,
∴BH=2,
∵AB∥x轴,
∴B(2,4),S△AOB=
=10
故答案为:(2,4),10.
(2)四边形AOCB是菱形.
∵△ABO沿直线OB翻折得到△CBO,
∴OB垂直平分AC,
∴OC=OA,BC=AB,
∴OC=OA=BC=AB,
∴四边形AOCB是菱形.
(3)∵OC=OA=5,
∴C(5,0),设直线AC的解析式为y=kx+b,则
,解得,
,
直线AC的解析式为:y=-
x+
,
∴当x=0时,y=
,
∴M(0,
),
∴OM=
,HM=
如图2,当P点在AB边上运动时,
∴S=
BP•HM=
(5-2t)×
=-
t+
(0≤t<
)
∵-
<0,
∴当t=0时,S有最大值
,
当t=
时,点P与B点重合,△PMB不存在,S=0.
∵四边形AOCB是菱形,
∴MB=MO,∠MBC=∠MOC=90°,
如图3,当P点在BC边上运动时,
∴S=
BP•BM=
(2t-5)×
,
S=
t-
(
<t≤5)
∵
>0,
∴当t=5时,S有最大值
,
综上所述,当t=5时,S有最大值
.
(4)设OP与AC相交于F,连接OB交AC于点D.
∵四边形AOCB是菱形,
∴∠AOC=∠ABC,∠BOC=∠ABO,∠BAO=∠BCO,
∴∠AOM=∠ABM.
∵∠MPB+∠BCO=90°,
∴∠MPB+∠BAO=90°
∵∠BAO+∠AOM=90°
∴∠MPB=∠AOM=∠ABM.
如图4,当点P在AB上运动时,
∵∠MPB=∠ABM.,OH⊥AB
∴PH=HB=5-3=2,PA=1,
∴t=
∵△AFP∽△CFO,
∴
=
=
,
∴AF=
AC
在Rt△AEC和△OBH中,由勾股定理,得
AC=4
,OB=2
,
∴AF=
×4
=
,
∴CF=
,
∵四边形ABCO是菱形,
∴AC⊥OB,OD=BD=
,AD=CD=2
,
∴FD=2
-
=
,
∴tan∠OFC=
=
=
如图5,当P在BC上运动时,
∵∠BHM=∠PBM=90°,∠MPB+∠BMP=90°,∠MPB+∠BCO=90°,
∴∠BMP=∠BCO=∠BAO,
∵∠AOM=∠ABM,且∠ABM+∠BMH=90°,∠AOM+∠BAO=90°,
∴∠BMH=∠BAO=∠BCO=∠BMP,即∠BMH=∠BMP,
∴△BHM∽△PBM,
∴
=
,
∴
=
,
∴BP=
,
∴PC=5-
=
,
∴t=
=
,
∵PC∥OA,
∴△PFC∽△OFA,
∴
=
=
=
,
∴CF=
AC=
,
∴FD=CD-CF=2
-
=
,
∴tan∠OFD=
=
=1
综上所述,当t=
时,直线OP与直线AC所夹锐角的正切值为
,当t=
时,直线OP与直线AC所夹锐角的正切值为1
 解:(1)如图1,作AT⊥x轴于点T,
解:(1)如图1,作AT⊥x轴于点T,∴∠ATO=90°,
∵A(-3,4),
∴AT=4,TO=3,在Rt△AOT中由勾股定理,得
AO=
| 9+16 |
∵AB=AO,
∴AO=5,
∴BH=2,
∵AB∥x轴,
∴B(2,4),S△AOB=
| 5×4 |
| 2 |
故答案为:(2,4),10.
(2)四边形AOCB是菱形.
∵△ABO沿直线OB翻折得到△CBO,
∴OB垂直平分AC,
∴OC=OA,BC=AB,
∴OC=OA=BC=AB,
∴四边形AOCB是菱形.
(3)∵OC=OA=5,
∴C(5,0),设直线AC的解析式为y=kx+b,则
|
|
直线AC的解析式为:y=-
| 1 |
| 2 |
| 5 |
| 2 |
∴当x=0时,y=
| 5 |
| 2 |
∴M(0,
| 5 |
| 2 |
∴OM=
| 5 |
| 2 |
| 3 |
| 2 |
如图2,当P点在AB边上运动时,

∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 3 |
| 2 |
| 15 |
| 4 |
| 5 |
| 2 |
∵-
| 3 |
| 2 |
∴当t=0时,S有最大值
| 15 |
| 4 |
当t=
| 5 |
| 2 |
∵四边形AOCB是菱形,
∴MB=MO,∠MBC=∠MOC=90°,
如图3,当P点在BC边上运动时,

∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
S=
| 5 |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
∵
| 5 |
| 2 |
∴当t=5时,S有最大值
| 25 |
| 4 |
综上所述,当t=5时,S有最大值
| 25 |
| 4 |
(4)设OP与AC相交于F,连接OB交AC于点D.
∵四边形AOCB是菱形,
∴∠AOC=∠ABC,∠BOC=∠ABO,∠BAO=∠BCO,
∴∠AOM=∠ABM.
∵∠MPB+∠BCO=90°,
∴∠MPB+∠BAO=90°
∵∠BAO+∠AOM=90°
∴∠MPB=∠AOM=∠ABM.
如图4,当点P在AB上运动时,

∵∠MPB=∠ABM.,OH⊥AB
∴PH=HB=5-3=2,PA=1,
∴t=
| 1 |
| 2 |
∵△AFP∽△CFO,
∴
| AF |
| CF |
| AP |
| CO |
| 1 |
| 5 |
∴AF=
| 1 |
| 6 |
在Rt△AEC和△OBH中,由勾股定理,得
AC=4
| 5 |
| 5 |
∴AF=
| 1 |
| 6 |
| 5 |
| 2 |
| 3 |
| 5 |
∴CF=
| 10 |
| 3 |
| 5 |
∵四边形ABCO是菱形,
∴AC⊥OB,OD=BD=
| 5 |
| 5 |
∴FD=2
| 5 |
| 2 |
| 3 |
| 5 |
| 4 |
| 3 |
| 5 |
∴tan∠OFC=
| OD |
| FD |
| ||||
|
| 3 |
| 4 |
如图5,当P在BC上运动时,
∵∠BHM=∠PBM=90°,∠MPB+∠BMP=90°,∠MPB+∠BCO=90°,
∴∠BMP=∠BCO=∠BAO,

∵∠AOM=∠ABM,且∠ABM+∠BMH=90°,∠AOM+∠BAO=90°,
∴∠BMH=∠BAO=∠BCO=∠BMP,即∠BMH=∠BMP,
∴△BHM∽△PBM,
∴
| HB |
| PB |
| HM |
| BM |
∴
| 2 |
| PB |
| ||
|
∴BP=
| 10 |
| 3 |
∴PC=5-
| 10 |
| 3 |
| 5 |
| 3 |
∴t=
5+
| ||
| 2 |
| 25 |
| 6 |
∵PC∥OA,
∴△PFC∽△OFA,
∴
| CF |
| AF |
| PC |
| OA |
| ||
| 5 |
| 1 |
| 3 |
∴CF=
| 1 |
| 4 |
| 5 |
∴FD=CD-CF=2
| 5 |
| 5 |
| 5 |
∴tan∠OFD=
| OD |
| DF |
| ||
|
综上所述,当t=
| 1 |
| 2 |
| 3 |
| 4 |
| 25 |
| 6 |
点评:本题考查了相似三角形的判定与性质,坐标与图形的性质,待定系数法求一次函数的解析式,菱形的判定,图形的翻折变换,锐角三角函数的运用及勾股定理的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
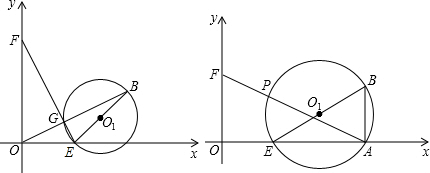
 已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.
已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.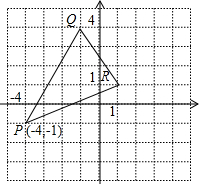 已知△PQR在直角坐标系中的位置如图所示:
已知△PQR在直角坐标系中的位置如图所示: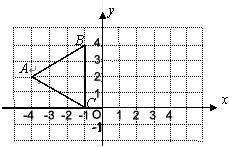 (2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
(2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )