探究与应用: A 在锐角△ABC中,∠A.∠B.∠C的对边分别是a.b.c.过A作AD⊥BC.垂足为D.则sinB=A——青夏教育精英家教网——

摘要：探究与应用: A 在锐角△ABC中,∠A.∠B.∠C的对边分别是a.b.c.过A作AD⊥BC.垂足为D.则sinB=AD/c.sinC=AD/B.AD=csinB.AD=bsinC. b 于是csinB.AD=bsinC.即 b/sinB=c/sinC . c 同理.有a/sinA=c/sinC. a/sinA=b/sinB . a B D C 所以 a/sinA =b/sinB=c/sinC . (* ) 图1 即在一个三角形中.各边和它所对角的正弦的比相等. 求出用关系式 (1)在锐角三角形中.若已知三个元素a.b.∠A.运用上述结论(*)和有关定理就可以求出其余三个未知元素c.∠B.∠C.请你按照下列步骤填空.完成求解过程: 第一步:由条件a.b.∠A ∠B, 求出用关系式第二步:由条件∠A.∠B ∠C, 求出用关系式第三步:由条件 c, (2)一货轮在C处测得灯塔A在货轮的北偏西30°的方向上.随后货轮以28.4海里/小时的速度向北偏东45°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西70°的方向上,求此时货轮距灯塔A的距离AB 北 (参考数据:sin40°=0.643,sin65°=0.906,sin70°=0.940,sin75°=0.966.)

网址：http://m.1010jiajiao.com/timu3_id_444941[举报]

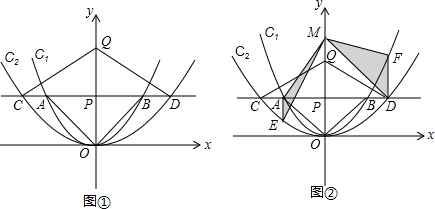
（2013•吉林）如图①，在平面直角坐标系中，点P（0，m²）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C₁：y=

x²于点A、B，交抛物线C₂：y=

x²于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
【猜想与证明】
填表：

由上表猜想：对任意m（m＞0）均有

．请证明你的猜想．
【探究与应用】
（1）利用上面的结论，可得△AOB与△CQD面积比为

；
（2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C₂于点E，过点D作y轴的平行线交抛物线C₁于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为

查看习题详情和答案>>

探究与应用²
1+3+5=（　　）²
1+3+5+7=（　　）²
1+3+5+7+9=（　　）²
1+3+5+7+9+11=（　　）²
…
问题：
（1）在括号内填上适当的数；
（2）用一句简练、准确的语言概括此计算规律或写出一个能反映此计算一般规律的式子；
（3）根据规律计算：（-1）+（-3）+（-5）+…+（-99）查看习题详情和答案>>

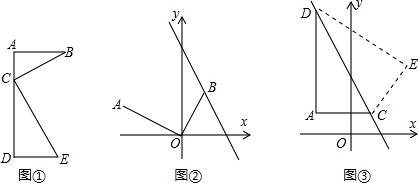
探究与应用：在学习几何时，我们可以通过分离和构造基本图形，将几何“模块”化．例如在相似三角形中，K字形是非常重要的基本图形，可以建立如下的“模块”（如图①）：
（1）请就图①证明上述“模块”的合理性．已知：∠A=∠D=∠BCE=90°，求证：△ABC∽△DCE；
（2）请直接利用上述“模块”的结论解决下面两个问题：
①如图②，已知点A（-2，1），点B在直线y=-2x+3上运动，若∠AOB=90°，求此时点B的坐标；
②如图③，过点A（-2，1）作x轴与y轴的平行线，交直线y=-2x+3于点C、D，求点A关于直线CD的对称点E的坐标．

查看习题详情和答案>>

（2012•南关区模拟）思考与推理
如图①，在矩形ABCD中，点E为CD的中点，连接AE并延长交BC的延长线于点F，过点E作EM⊥AF交BC于点M，连接AM，请思考并判断AE与EF、∠1与∠2具有怎样的数量关系？并推理说明你的判断
探究与应用
如图②，在梯形ABCD中，点E为CD的中点，连接AE，过点E作EM⊥AE交BC于点M，连接AM．若∠EMC=70°，则∠DAE=

查看习题详情和答案>>

（2013•太仓市二模）探究与应用．试完成下列问题：
（1）如图①，已知等腰Rt△ABC中，∠C=90°，点O为AB的中点，作∠POQ=90°，分别交AC、BC于点P、Q，连结PQ、CO，求证：AP²+BQ²=PQ²；
（2）如图②，将等腰Rt△ABC改为任意直角三角形，点O仍为AB的中点，∠POQ=90°，试探索上述结论AP²+BQ²=PQ²是否仍成立；
（3）通过上述探究（可直接运用上述结论），试解决下面的问题：如图③，已知Rt△ABC中，∠C=90°，AC=6，BC=8，点O为AB的中点，过C、O两点的圆分别交AC、BC于P、Q，连结PQ，求△PCQ面积的最大值．

查看习题详情和答案>>