题目内容
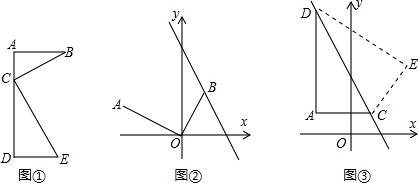
探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
(1)请就图①证明上述“模块”的合理性.已知:∠A=∠D=∠BCE=90°,求证:△ABC∽△DCE;
(2)请直接利用上述“模块”的结论解决下面两个问题:
①如图②,已知点A(-2,1),点B在直线y=-2x+3上运动,若∠AOB=90°,求此时点B的坐标;
②如图③,过点A(-2,1)作x轴与y轴的平行线,交直线y=-2x+3于点C、D,求点A关于直线CD的对称点E的坐标.
(1)请就图①证明上述“模块”的合理性.已知:∠A=∠D=∠BCE=90°,求证:△ABC∽△DCE;
(2)请直接利用上述“模块”的结论解决下面两个问题:
①如图②,已知点A(-2,1),点B在直线y=-2x+3上运动,若∠AOB=90°,求此时点B的坐标;
②如图③,过点A(-2,1)作x轴与y轴的平行线,交直线y=-2x+3于点C、D,求点A关于直线CD的对称点E的坐标.

分析:(1)根据余角的性质就可以求出∠B=∠DCE,再由∠A=∠D=90°,就可以得出结论;
(2)①作AG⊥x轴于点G,BH⊥x轴于点H,可以得出△AGO∽△OHB,可以得出
=
,设点B的坐标为(x,-2x+3),建立方程求出其解就可以得出结论;
②过点E作EN⊥AC的延长线于点N,过点D作DM⊥NE的延长线于点M,设E(x,y),先可以求出C、D的坐标,进而可以求出DM=x+2,ME=7-y,CN=x-1,EN=y-1,DE=AD=6,CE=AC=3.再由条件可以求出△DME∽△ENC,利用相似三角形的性质建立方程组求出其解就可以得出结论.
(2)①作AG⊥x轴于点G,BH⊥x轴于点H,可以得出△AGO∽△OHB,可以得出
| AG |
| OH |
| GO |
| BH |
②过点E作EN⊥AC的延长线于点N,过点D作DM⊥NE的延长线于点M,设E(x,y),先可以求出C、D的坐标,进而可以求出DM=x+2,ME=7-y,CN=x-1,EN=y-1,DE=AD=6,CE=AC=3.再由条件可以求出△DME∽△ENC,利用相似三角形的性质建立方程组求出其解就可以得出结论.
解答:(1)证明:∵∠BCE=90°,
∴∠ACB+∠DCE=90°.
∵∠A=90°,
∴∠ACB+∠B=90°,
∴∠DCE=∠B.
∵∠A=∠D,
∴△ABC∽△DCE;
(2)解:①作AG⊥x轴于点G,BH⊥x轴于点H,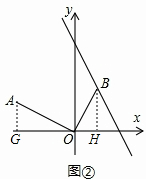
∴△AGO∽△OHB,
∴
=
.
∵A(-2,1),
∴AG=1,GO=2.
∵点B在直线y=-2x+3上,
∴设点B的坐标为(x,-2x+3),
∴OH=x,BH=-2x+3,
∴
=
,
∴x=
,
∴-2x+3=
,
∴B(
,
);
②过点E作EN⊥AC的延长线于点N,过点D作DM⊥NE的延长线于点M,
∵A(-2,1),
∴C点的纵坐标为1,D点的横坐标为-2,
∴1=-2x+3,y=-2×(-2)+3,
∴x=1,y=7,
∴C(1,1),D(-2,7).
设E(x,y),
∴DM=x+2,ME=7-y,CN=x-1,EN=y-1,
由对称可知:DE=AD=6,CE=AC=3.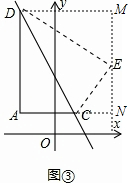
∵∠M=∠N=∠DEC=90°,
∴△DME∽△ENC,
∴
=
=
,
∴
,
∴解得:
∴E(
,
).
∴∠ACB+∠DCE=90°.
∵∠A=90°,
∴∠ACB+∠B=90°,
∴∠DCE=∠B.
∵∠A=∠D,
∴△ABC∽△DCE;
(2)解:①作AG⊥x轴于点G,BH⊥x轴于点H,

∴△AGO∽△OHB,
∴
| AG |
| OH |
| GO |
| BH |
∵A(-2,1),
∴AG=1,GO=2.
∵点B在直线y=-2x+3上,
∴设点B的坐标为(x,-2x+3),
∴OH=x,BH=-2x+3,
∴
| 1 |
| x |
| 2 |
| -2x+3 |
∴x=
| 3 |
| 4 |
∴-2x+3=
| 3 |
| 2 |
∴B(
| 3 |
| 4 |
| 3 |
| 2 |
②过点E作EN⊥AC的延长线于点N,过点D作DM⊥NE的延长线于点M,
∵A(-2,1),
∴C点的纵坐标为1,D点的横坐标为-2,
∴1=-2x+3,y=-2×(-2)+3,
∴x=1,y=7,
∴C(1,1),D(-2,7).
设E(x,y),
∴DM=x+2,ME=7-y,CN=x-1,EN=y-1,
由对称可知:DE=AD=6,CE=AC=3.

∵∠M=∠N=∠DEC=90°,
∴△DME∽△ENC,
∴
| DM |
| EN |
| ME |
| CN |
| DE |
| CE |
∴
|
∴解得:
|
∴E(
| 14 |
| 5 |
| 17 |
| 5 |
点评:本题是一道一次函数的综合试题,考查了相似三角形的判定及性质的运用,轴对称的性质的运用,方程组的运用,解答时灵活运用相似三角形的性质是关键.

练习册系列答案
相关题目