摘要:抛物线Y= -X+ 与Y轴交于点. ( 1 )求出 m 的值并画出这条抛物线, ( 2 )求它与 x 轴的交点和抛物线顶点的坐标, . ( 3 ) x 取什么值时.抛物线在X轴上方? ( 4 )X取什么值时.Y的值随 x 值的增大而减小? 第21题图
网址:http://m.1010jiajiao.com/timu3_id_444255[举报]
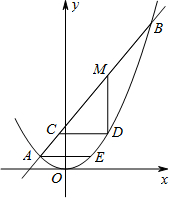
如图,抛物线:![]() 与
与![]() 轴交于点A(-2,0)和B(4,0)、与
轴交于点A(-2,0)和B(4,0)、与![]() 轴交于点C.
轴交于点C.
(1)求抛物线的解析式;
(2![]() )T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿![]() 轴同时出发相向而行.当点M到原点时,点Q立刻掉头并以每秒
轴同时出发相向而行.当点M到原点时,点Q立刻掉头并以每秒![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.

抛物线y=x2在直角坐标系中向下平移4个单位得到抛物线y1,y1与x轴的交点为A1、B1,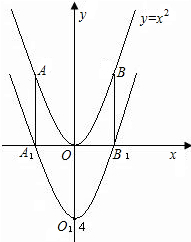 与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.
与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.
(1)写出y1的解析式及A、B两点的坐标;
(2)求抛物线Y和y1及线段AA1和BB1围成的图形的面积;
(3)若平行于x轴的一条直线y=m与抛物线y交于P、Q两点,与抛物线y1交于R、S两点,且P、Q两点三等分线段RS,求m的值;
(4)若正比例函数y=kx(k≠0)与抛物线y1交于M、N两点,问点O能否平分线段MN,并说明理由. 查看习题详情和答案>>
 与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.
与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.(1)写出y1的解析式及A、B两点的坐标;
(2)求抛物线Y和y1及线段AA1和BB1围成的图形的面积;
(3)若平行于x轴的一条直线y=m与抛物线y交于P、Q两点,与抛物线y1交于R、S两点,且P、Q两点三等分线段RS,求m的值;
(4)若正比例函数y=kx(k≠0)与抛物线y1交于M、N两点,问点O能否平分线段MN,并说明理由. 查看习题详情和答案>>
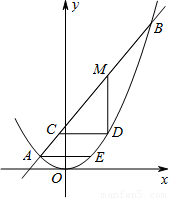
 .
.
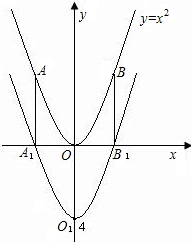 与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.
与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.