题目内容
抛物线y=x2在直角坐标系中向下平移4个单位得到抛物线y1,y1与x轴的交点为A1、B1,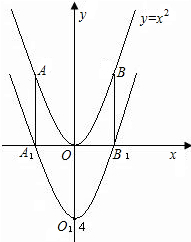 与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.
与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.(1)写出y1的解析式及A、B两点的坐标;
(2)求抛物线Y和y1及线段AA1和BB1围成的图形的面积;
(3)若平行于x轴的一条直线y=m与抛物线y交于P、Q两点,与抛物线y1交于R、S两点,且P、Q两点三等分线段RS,求m的值;
(4)若正比例函数y=kx(k≠0)与抛物线y1交于M、N两点,问点O能否平分线段MN,并说明理由.
分析:(1)抛物线y=x2向下平移4个单位得抛物线y1,故y的顶点向下平移4个单位.故能得到解析式,令y=0,就能求得A、B两点的坐标.(2)连接AB,则抛物线y1和A1B1围成的图形的面积等于抛物线y和AB围成的图形的面积,故抛物线y1和y2及AA1图1和BB1围成的图形的面积等于正方形AA1BB1的面积.(3)由RP=PQ=QS,可得RS=3PQ.进而求得m.(4)看点O能否平分线段MN,两图象交点横坐标之和是不是等于0.
解答:解:(1)抛物线y=x2向下平移4个单位得抛物线y1,
故y的顶点向下平移4个单位,
可得y1=x2-4,令y=0,求得x=±2,
故坐标A(-2,4)、B(2,4).
(2)连接AB,则抛物线y1和A1B1围成的图形的面积等于
抛物线y和AB围成的图形的面积,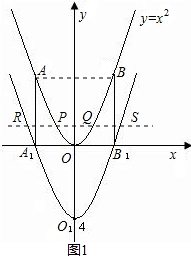
∴抛物线y1和y2及AA1图1和BB1围成的图形的面积等于正方形AA1BB1的面积S=16.
(3)如图1,
∵RP=PQ=QS,
∴RS=3PQ,
即2
=6
,解得m=
.
(4)如图2,点O不能平分线段MN,理由如下:
由
,得x2-kx-4=0,
∴x1+x2=k≠0,
∴x1≠-x2,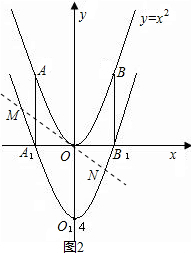
∴OM≠ON.
故y的顶点向下平移4个单位,
可得y1=x2-4,令y=0,求得x=±2,
故坐标A(-2,4)、B(2,4).
(2)连接AB,则抛物线y1和A1B1围成的图形的面积等于
抛物线y和AB围成的图形的面积,

∴抛物线y1和y2及AA1图1和BB1围成的图形的面积等于正方形AA1BB1的面积S=16.
(3)如图1,
∵RP=PQ=QS,
∴RS=3PQ,
即2
| m+4 |
| 4 |
| 1 |
| 2 |
(4)如图2,点O不能平分线段MN,理由如下:
由
|
∴x1+x2=k≠0,
∴x1≠-x2,

∴OM≠ON.
点评:本题是二次函数的综合题,会求抛物线的解析式,涉及平移等知识点.此题不难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

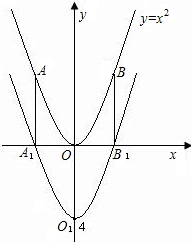 与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.
与y轴的交点为O1,A1、B1、O1对应y=x2上的点依次为A、B、O.
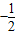 时,
时,