题目内容
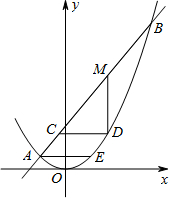
抛物线y=ax2和直线y=kx+b(k为正常数)交于点A和点B,其中点A的坐标是(-2,1),过点A作x轴的平行线交抛物线于点E,点D是抛物线上B.E之间的一个动点,设其横坐标为t,经过点D作两坐标轴的平行线分别交直线AB于点C.B,设CD=r,MD=m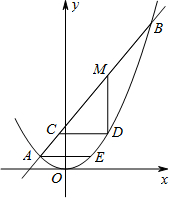 .
.
(1)根据题意可求出a=______,点E的坐标是______.
(2)当点D可与B、E重合时,若k=0.5,求t的取值范围,并确定t为何值时,r的值最大;
(3)当点D不与B、E重合时,若点D运动过程中可以得到r的最大值,求k的取值范围,并判断当r为最大值时m的值是否最大,说明理由.(下图供分析参考用)
 解:(1)根据题意知,点A(-2,1)在抛物线y=ax2上,
解:(1)根据题意知,点A(-2,1)在抛物线y=ax2上,∴1=(-2)2a,
解得,a=
 .
.∵抛物线y=ax2关于y轴对称,AE∥x轴,
∴点A、E关于y轴对称,
∴E(2,1).
故答案是:
 ,(2,1).
,(2,1).(2)∵点A(-2,1)在直线y=kx+b(k为正常数)上,k=0.5,
∴1=-2×0.5+b,
解得,b=2,
即直线AB的解析式为y=
 x+2.
x+2.∵由(1)知,抛物线的解析式y=
 x2,抛物线y=
x2,抛物线y= x2和直线y=
x2和直线y= x+2(k为正常数)交于点A和点B,
x+2(k为正常数)交于点A和点B,∴
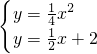 ,
,解得,
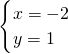 或
或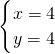 ,
,∴它们的交点坐标是(-2,1),(4,4),即B(4,4).
当点D与点E重合时,t=2.当点D与点B重合时,t=4,
∴t的取值范围是:2≤t≤4.
∵点C在直线y=
 x+2上,点D在抛物线y=
x+2上,点D在抛物线y= x2上,CD∥x轴,
x2上,CD∥x轴,∴D(t,
 t2),C(
t2),C(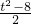 ,
, t2),
t2),∴r=t-
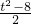 =-
=- (t-1)2+
(t-1)2+ (2≤t≤4).
(2≤t≤4).∵在2≤t≤4范围内,r随t的增大而减小,
∴当t=2时,r最大=4.即当t=2时,r取最大值.
(3)∵点A、B是直线与抛物线的交点,
∴kx+b=
 x2,即x2-4kx-4b=0,
x2,即x2-4kx-4b=0,∴xA+xB=4k.
∵xA=-2,
∴xB=4k+2.
又∵点D不与B、E重合,
∴2<t<4k+2.
设D(t,
 t2),则点C的纵坐标为
t2),则点C的纵坐标为 t2,将其代入y=kx+b中,得x=
t2,将其代入y=kx+b中,得x=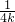 t2-
t2- ,
,∴点C的坐标为(
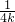 t2-
t2- ,
, t2),
t2),∴r=CD=t-(
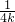 t2-
t2- )=-
)=-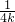 (t-2k)2+k+
(t-2k)2+k+ ,
,当t=2k时,r取最大值.
∴2<2k<4k+2,
解得,k>1.
又∵k=
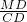 =
= ,
,∴m=kr=-
 (t-2k)2+k2+b,
(t-2k)2+k2+b,∴当t=2k时,m的值也最大.
综上所述,当r为最大值时m的值也是最大.
分析:(1)利用二次函数图象上点的坐标特征知,点A的坐标满足抛物线的解析式,所以把点A的坐标代入抛物线的解析式,即可求得a的值;由抛物线y=ax2的对称性知,点A、点E关于y轴对称;
(2)根据抛物线与直线的解析式求得点B的坐标为(4,4),则t的最小值是点E的横坐标,t的最大值是点B的横坐标;由于点C在直线y=
 x+2上,点D在抛物线y=
x+2上,点D在抛物线y= x2上,CD∥x轴,所以D(t,
x2上,CD∥x轴,所以D(t, t2),C(
t2),C(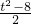 ,
, t2);最后由两点间的距离公式求得r=|
t2);最后由两点间的距离公式求得r=| (t-1)2-
(t-1)2- |(2≤t≤4),所以根据二次函数最值的求法来求当r取最大值时t的值;
|(2≤t≤4),所以根据二次函数最值的求法来求当r取最大值时t的值;(3)①设D(t,
 t2).由一次函数、二次函数图象上点的坐标特征求得点C的坐标为(
t2).由一次函数、二次函数图象上点的坐标特征求得点C的坐标为(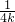 t2-
t2- ,
, t2).然后根据两点间的距离公式知r=-
t2).然后根据两点间的距离公式知r=-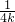 (t-2k)2+k+
(t-2k)2+k+ ,易知当t=2k时,r取最大值.
,易知当t=2k时,r取最大值.②根据一次函数y=kx+b中的k的几何意义知k=
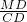 =
= ,即m=kr=-
,即m=kr=- (t-2k)2+k2+b,显然,当t=2k时,m取最大值.
(t-2k)2+k2+b,显然,当t=2k时,m取最大值.点评:本题考查了二次函数综合题.其中涉及到的知识点由待定系数法求一次函数、二次函数的解析式,一次函数(二次函数)图象上点的坐标特征,二次函数最值的求法等.求二次函数最值时,此题采用了“配方法”.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 .
.