摘要:4.注意:(1)垂径定理及其推论是指:一条弦①在“过圆心 ②“垂直于另一条弦 ③“平分这另一条弦 ④“平分这另一条弦所对的劣弧 ⑤“ 平分这另一条弦所对的优弧 的五个条件中任意具有两个条件.则必具有另外三个结论(当①③为条件时要对另一条弦增加它不是直径的限制).条理性的记忆.不但简化了对它实际代表的10条定理的记忆且便于解题时的灵活应用.垂径定理提供了证明线段相等.角相等.垂直关系等的重要依据,(2)有弦可作弦心距组成垂径定理图形,见到直径要想到它所对的圆周角是直角.想垂径定理,想到过它的端点若有切线.则与它垂直.反之.若有垂线则是切线.想到它被圆心所平分,(3)见到四个点在圆上想到有4组相等的同弧所对的圆周角.要想到应用圆内接四边形的性质.(4)等弧的概念等.
网址:http://m.1010jiajiao.com/timu3_id_444096[举报]
垂径定理及其推论:
定理:垂直于弦的直径
推论:
(1)平分弦(不是直径)的直径
(2)弦的垂直垂直平分线经过圆心,并且
(3)平分弦所对的一条弧的直径,垂直平分弦,并且
查看习题详情和答案>>
定理:垂直于弦的直径
平分弦,并且平分弦所对的两条弧
平分弦,并且平分弦所对的两条弧
.推论:
(1)平分弦(不是直径)的直径
垂直于弦,并且平分弦所对的两条弧
垂直于弦,并且平分弦所对的两条弧
.(2)弦的垂直垂直平分线经过圆心,并且
平分弦所对的两条弧
平分弦所对的两条弧
.(3)平分弦所对的一条弧的直径,垂直平分弦,并且
平分弦所对的另一条弧
平分弦所对的另一条弧
.垂径定理及其推论:
定理:垂直于弦的直径______.
推论:
(1)平分弦(不是直径)的直径______.
(2)弦的垂直垂直平分线经过圆心,并且______.
(3)平分弦所对的一条弧的直径,垂直平分弦,并且______.
查看习题详情和答案>>
垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,假命题是( )
A.①②![]() ③④ B.①③
③④ B.①③![]() ②④
②④
C.①④![]() ②③ D.②③
②③ D.②③![]() ①④
①④
如图,△![]() 内接于⊙
内接于⊙![]() ,点
,点![]() 在
在![]() 的延长线上,sinB=
的延长线上,sinB=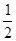 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: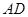 是⊙
是⊙![]() 的切线;⑵若
的切线;⑵若![]() ,求
,求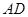 的长。
的长。
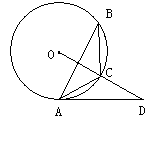
【解析】(1)连接OA,由于sinB=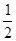 ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
(2)由于OC⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠BAC=30°,于是有∠DAE=60°,∠D=30°,在Rt△ACE中,利用三角函数值可求AE,在Rt△ADE中利用30°的锐角所对的直角边等于斜边的一半,可求AD.
查看习题详情和答案>>
如图,△ 内接于⊙
内接于⊙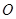 ,点
,点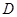 在
在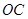 的延长线上,sinB=
的延长线上,sinB=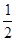 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: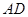 是⊙
是⊙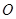 的切线;⑵若
的切线;⑵若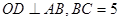 ,求
,求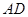 的长。
的长。
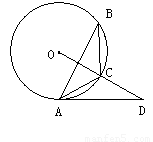
【解析】(1)连接OA,由于sinB=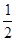 ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
(2)由于OC⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠BAC=30°,于是有∠DAE=60°,∠D=30°,在Rt△ACE中,利用三角函数值可求AE,在Rt△ADE中利用30°的锐角所对的直角边等于斜边的一半,可求AD.
查看习题详情和答案>>