题目内容
如图,△![]() 内接于⊙
内接于⊙![]() ,点
,点![]() 在
在![]() 的延长线上,sinB=
的延长线上,sinB=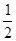 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: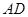 是⊙
是⊙![]() 的切线;⑵若
的切线;⑵若![]() ,求
,求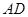 的长。
的长。
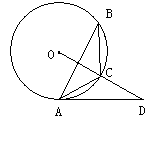
【解析】(1)连接OA,由于sinB=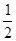 ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
(2)由于OC⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠BAC=30°,于是有∠DAE=60°,∠D=30°,在Rt△ACE中,利用三角函数值可求AE,在Rt△ADE中利用30°的锐角所对的直角边等于斜边的一半,可求AD.
(1)是⊙
![]() 的切线
的切线
(1)证明:如图,连接OA
∵sinB= ∴∠B=30°∴∠AOC=60°.
又OA=OC ∴△AOC为等边三角形,∴∠OAC=60°.
又∠CAD=30°, ∴∠OAD=∠OAC+∠CAD=60°+30°=90°
∴OA⊥AD , ∴AD是⊙O的切线。…………………4分
(2)∵OD⊥AB, ∴=
∴AC=BC=5
由(1)知:OA=AC, ∴OA=5………………………6分
在RT△OAD中, tan∠AOD= ,
∴AD=OA ·tan∠AOD=5 ·tan60°=5……………8分

练习册系列答案
相关题目
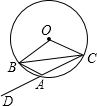 如图,△ABC内接于⊙O,点D是CA延长线上一点,若∠BOC=120°,则∠BAD=( )
如图,△ABC内接于⊙O,点D是CA延长线上一点,若∠BOC=120°,则∠BAD=( )| A、30° | B、60° | C、75° | D、90° |
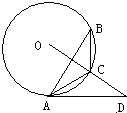 23、如图,△ABC内接于⊙O,点D在OC的延长线上,且∠B=∠CAD=30°,试判定AD与⊙O的位置关系,并说明理由.
23、如图,△ABC内接于⊙O,点D在OC的延长线上,且∠B=∠CAD=30°,试判定AD与⊙O的位置关系,并说明理由. (2012•南昌模拟)如图,△ABC内接于⊙O,点D在OC的延长线上,已知:∠B=∠CAD=30°.
(2012•南昌模拟)如图,△ABC内接于⊙O,点D在OC的延长线上,已知:∠B=∠CAD=30°.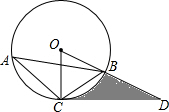 如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°,
如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°,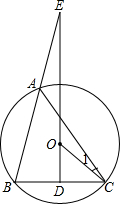 如图,△ABC内接于⊙O,点E是⊙O外一点,EO⊥BC于点D.
如图,△ABC内接于⊙O,点E是⊙O外一点,EO⊥BC于点D.