摘要：1．圆的点集定义及点和圆的位置关系
网址：http://m.1010jiajiao.com/timu3_id_444093[举报]
（2013•燕山区一模）定义：对于平面直角坐标系中的任意线段AB及点P，任取线段AB上一点Q，线段PQ长度的最小值称为点P到线段AB的距离，记作d（P→AB）．
已知O为坐标原点，A（4，0），B（3，3），C（m，n），D（m+4，n）是平面直角坐标系中四点．根据上述定义，解答下列问题：
（1）点A到线段OB的距离d（A→OB）=
（2）已知点G到线段OB的距离d（G→OB）=
，且点G的横坐标为1，则点G的纵坐标为
（3）当m的值变化时，点A到动线段CD的距离d （A→CD）始终为2，线段CD的中点为M．
①在图（2）中画出点M随线段CD运动所围成的图形并求出该图形的面积．
②点E的坐标为（0，2），m＞0，n＞0，作MH⊥x轴，垂足为H．是否存在m的值，使得以A、M、H为顶点的三角形与△AOE相似？若存在，求出m的值；若不存在，请说明理由．
查看习题详情和答案>>
已知O为坐标原点，A（4，0），B（3，3），C（m，n），D（m+4，n）是平面直角坐标系中四点．根据上述定义，解答下列问题：
（1）点A到线段OB的距离d（A→OB）=
2
| 2 |
2
；| 2 |
（2）已知点G到线段OB的距离d（G→OB）=
| 5 |
1-
或1+
| 10 |
| 10 |
1-
或1+
．| 10 |
| 10 |
（3）当m的值变化时，点A到动线段CD的距离d （A→CD）始终为2，线段CD的中点为M．
①在图（2）中画出点M随线段CD运动所围成的图形并求出该图形的面积．
②点E的坐标为（0，2），m＞0，n＞0，作MH⊥x轴，垂足为H．是否存在m的值，使得以A、M、H为顶点的三角形与△AOE相似？若存在，求出m的值；若不存在，请说明理由．
如图（1），抛物线y=x2-2x+k与x轴交于A、B两点，与y轴交于点C（0，-3）． （注：图（2）、图（3）为解答备用图）
（1）求k值及A和B的坐标；
（2）设抛物线y=x2-2x+k与的顶点为M，求四边形ABMC的面积；
（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；
（4）在抛物线y=x2-2x+k与上求点Q，使△BCQ是以BC为直角边的直角三角形．
查看习题详情和答案>>
（1）求k值及A和B的坐标；
（2）设抛物线y=x2-2x+k与的顶点为M，求四边形ABMC的面积；
（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；
（4）在抛物线y=x2-2x+k与上求点Q，使△BCQ是以BC为直角边的直角三角形．
查看习题详情和答案>>
如图，在矩形ABCD中，AB=4，AD=5，P是BC边上的一个动点，PE⊥AP，PE交DC于点E，AE交BC的延长线于点F．（1）求证：①△PCE∽△ABP；②CE•AB=PC•BP；
（2）当FC=3时，求EC、BP的长及△PCE和△ABP的面积比．
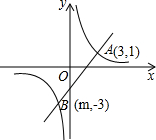如图，一次函数y=kx+b的图象与反比例函数
次函数y=x+a交于点A和点D．