（2013•江宁区一模）A、B两地相距630千米，客车、货车分别从A、B两地同时出发，匀速相向行驶（客车的终点站是C站，货车的终点站是A站）．客车需9小时到达C站，货车2小时可到达途中C站（如图1所示）．货车的速度是客车的 

3

4

，客车、货车到C站的距离分别为y₁、y₂（千米），它们与行驶时间x（小时）之间的函数关系（如图2所示）．

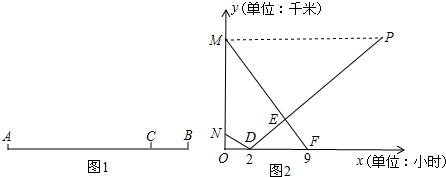
（1）客车的速度是千米/小时，货车的速度是千米/小时；
（2）P点坐标的实际意义是；
（3）求两小时后，货车与C站的距离y₂与行驶时间x之间的函数关系式；
（4）求客车与货车同时出发后，经过多长时间两车相距360千米？

（2013•包头）如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．
（1）求证：PA是⊙O的切线；
（2）过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长；
（3）在满足（2）的条件下，若AF：FD=1：2，GF=1，求⊙O的半径及sin∠ACE的值．

（2013•和平区一模）如图，△ABC内接于⊙O，AD是∠ABC的平分线，交BC于点M，交⊙O于点D．则图中相似三角形共有（　　）

（2013•金山区二模）如图，已知在△ABC中，DE是AC的垂直平分线，交AC于点D，AB于点E，若BC=8，△BCE的周长为
21，cos∠B=

5

13

．
求：（1）AB的长；
   （2）AC的长．

（2013•永安市质检）A、B两地相距630千米，客车、货车分别从A、B两地同时出发，匀速相向行驶（客车的终点站是C站，货车的终点站是A站．客车需9小时到达C站，货车2小时可到达途中C站（如图1所示）．货车的速度是客车的

3

4

，客车、货车到C站的距离y（千米）与行驶时间x（小时）之间的函数关系如图2所示．
（1）客车的速度是千米/小时，货车的速度是千米/小时；点P的坐标为．
（2）求客车与货车出发后，经过多长时间两车相距360千米？