题目内容
（2013•金山区二模）如图，已知在△ABC中，DE是AC的垂直平分线，交AC于点D，AB于点E，若BC=8，△BCE的周长为21，cos∠B=
| 5 | 13 |
求：（1）AB的长；
（2）AC的长．
分析：（1）由DE为AC的垂直平分线，得到AE=CE，三角形BEC的周长为三边之和，等量代换得到结果为AB+BC，由周长减去BC即可求出AB的长；
（2）过A作AF垂直于BC，在直角三角形ABF中，由AB与cosB的值，利用锐角三角函数定义求出BF的长，进而利用勾股定理求出AF的长，由BC-BF求出FC的长，在直角三角形AFC中，利用勾股定理即可求出AC的长．
（2）过A作AF垂直于BC，在直角三角形ABF中，由AB与cosB的值，利用锐角三角函数定义求出BF的长，进而利用勾股定理求出AF的长，由BC-BF求出FC的长，在直角三角形AFC中，利用勾股定理即可求出AC的长．
解答：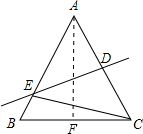
解：（1）∵DE是AC的垂直平分线，
∴AE=CE，
∵△BEC周长为BE+BC+EC=BE+AE+BC=AB+BC=21，BC=8，
∴AB=21-8=13；
（2）过A作AF⊥BC，
在Rt△ABF中，AB=13，cosB=
，
∴BF=ABcosB=5，FC=BC-BF=8-5=3，
∴根据勾股定理得：AF=
=12，
在Rt△AFC中，AF=12，FC=3，
根据勾股定理得：AC=
=
=3
．
解：（1）∵DE是AC的垂直平分线，∴AE=CE，
∵△BEC周长为BE+BC+EC=BE+AE+BC=AB+BC=21，BC=8，
∴AB=21-8=13；
（2）过A作AF⊥BC，
在Rt△ABF中，AB=13，cosB=
| 5 |
| 13 |
∴BF=ABcosB=5，FC=BC-BF=8-5=3，
∴根据勾股定理得：AF=
| AB2-BF2 |
在Rt△AFC中，AF=12，FC=3，
根据勾股定理得：AC=
| AF2+FC2 |
| 153 |
| 17 |
点评：此题属于解直角三角形题型，涉及的知识有：勾股定理，锐角三角函数定义，以及线段垂直平分线定理，熟练掌握定理是解本题的关键．
练习册系列答案
作业辅导系列答案
相关题目