摘要：1．重点:通过复习进一步使学生熟练利用有关概念.比例的性质.平行线分线段成比例定理及其推论.三角形一边平行线的性质和判定进行计算和证明.
网址：http://m.1010jiajiao.com/timu3_id_443807[举报]
要通过驾照考试，学开车的人就必须熟悉交通规则，也要知道当路况良好时，在干燥的路面上，使车停止前进所需的大约距离．若使车子停止前进的距离与车速之间的对应关系如下表所示．
(1)绘制使车子停止前进的距离相对于车速的图象．
(2)证明使车子停止前进的距离s(单位：m)、车速v(单位；km/h)有如下关系：
s＝
v＋
v2．
(3)在路况不良时，上表的停止距离需修正为45，72，105，144及189米，在这种情况下，要如何写出适当的公式？
查看习题详情和答案>>
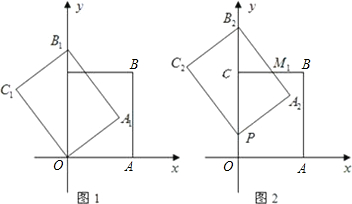
如图1，以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系，A点的坐标为（3，0），C点的坐标为（0，4）．将矩形OABC绕O点逆时针旋转，使B点落在y轴的正半轴上，旋转后的矩形为OA1B1C1，BC，A1B1相交于点M．
（1）求点B1的坐标与线段B1C的长；
（2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
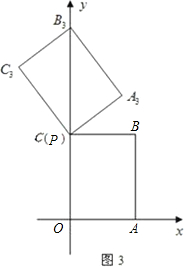
（3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．
查看习题详情和答案>>
（1）求点B1的坐标与线段B1C的长；
（2）将图1中的矩形OA1B1C1沿y轴向上平移，如图2，矩形PA2B2C2是平移过程中的某一位置，BC，A2B2相交于点M1，点P运动到C点停止．设点P运动的距离为x，矩形PA2B2C2与原矩形OABC重叠部分的面积为y，求y关于x的函数关系式，并写出x的取值范围；
（3）如图3，当点P运动到点C时，平移后的矩形为PA3B3C3．请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合，请简述你的做法．
查看习题详情和答案>>
如图，把矩形OABC放置在直角坐标系中，OA=6，OC=8，若将矩形折叠，使点B与O重合，得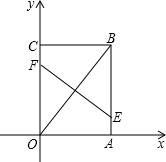
到折痕EF．
（1）可以通过 办法，使四边形AEFO变到四边形BEFC的位置（填“平移”、“旋转”或“翻转”）；
（2）写出点E在坐标系中的位置即点E的坐标 ；
（3）折痕EF的长为 ；
（4）若直线l把矩形OABC的面积分成相等的两部分，则直线l必经过点 ，写出经过这点的任意一条直线的函数关系式 ．
查看习题详情和答案>>
到折痕EF．（1）可以通过
（2）写出点E在坐标系中的位置即点E的坐标
（3）折痕EF的长为
（4）若直线l把矩形OABC的面积分成相等的两部分，则直线l必经过点
22、已知平面直角坐标系中有A（-2，1），B（2，3）两点．（1）在x轴上找一点M，使MA+MB最小，并求出点M的坐标；
（2）在x轴上找一点N，使得△ABN为等腰三角形，并通过画图说明使△ABN为等腰三角形的点N有多少个？
某班同学“五•一”期间组织外出爬山活动，花了230元租了一辆客车，如果参加活动的同学每人交7元租车费还不够，你明白这句话的含义吗？
典例分析：
例1在公路上，我们可以看到以下几种交通标志（如图），它们有着不同的意义．如果设汽车载重量为x吨，宽度为k米，高度为h米，速度为y千米/时，请你用不等式表示下列各种标志的意义．
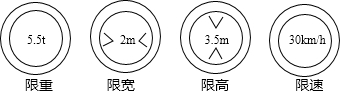
思路分析：由题意可知，限重、限宽、限高、限速中的“限”字的意义就是不超过，也就是“≤”的意义．这样，该题即可迎刃而解．
解：x≤5.5 k≤2 h≤3.5 y≤30
方法点拨：生活中的各种标志图、徽标等信息，现已成为考试中的一种素材，解决这类题目，需要将信息转化为数学语言，比如将“大于”“超过”“不超过”“非负数”“不大于”等等，准确“翻译”为数学符号．通过本题可以使我们认识到关注身边的数学的重要性．
例2用适当的不等式表示下列关系：
（1）x的4倍与2的和是非负数，可表示为 ．
（2）育才中学七年级一班学生数不到35人，设该班学生有x人，可表示为 ．
（3）人的寿命可超过120岁．设人的寿命为x岁，则可表示为 ．
（4）小林家有4口人，人均住房面积不足15平方米，则小林家的总住面积y平方米可表示为 ．
思路分析：（1）中的“非负数”即“≥0”的数；（2）中的“不到”即“＜”的意思；（3）中的“超过”即“＞”的意思；（4）中的“不足”即“＜”的意思．
答案：（1）4x+2≥0 （2）x＜35 （3）x＞120 （4）y＜60
方法点拨：做这种类型的题时，要善于把实际问题中的一些“不到”“大于”“超过”“不小于”等数学术语，准确迅速地转化为数学符号．此类题是为学生以后列不等式解应用题做铺垫的，所以必须掌握好． 查看习题详情和答案>>
典例分析：
例1在公路上，我们可以看到以下几种交通标志（如图），它们有着不同的意义．如果设汽车载重量为x吨，宽度为k米，高度为h米，速度为y千米/时，请你用不等式表示下列各种标志的意义．
思路分析：由题意可知，限重、限宽、限高、限速中的“限”字的意义就是不超过，也就是“≤”的意义．这样，该题即可迎刃而解．
解：x≤5.5 k≤2 h≤3.5 y≤30
方法点拨：生活中的各种标志图、徽标等信息，现已成为考试中的一种素材，解决这类题目，需要将信息转化为数学语言，比如将“大于”“超过”“不超过”“非负数”“不大于”等等，准确“翻译”为数学符号．通过本题可以使我们认识到关注身边的数学的重要性．
例2用适当的不等式表示下列关系：
（1）x的4倍与2的和是非负数，可表示为
（2）育才中学七年级一班学生数不到35人，设该班学生有x人，可表示为
（3）人的寿命可超过120岁．设人的寿命为x岁，则可表示为
（4）小林家有4口人，人均住房面积不足15平方米，则小林家的总住面积y平方米可表示为
思路分析：（1）中的“非负数”即“≥0”的数；（2）中的“不到”即“＜”的意思；（3）中的“超过”即“＞”的意思；（4）中的“不足”即“＜”的意思．
答案：（1）4x+2≥0 （2）x＜35 （3）x＞120 （4）y＜60
方法点拨：做这种类型的题时，要善于把实际问题中的一些“不到”“大于”“超过”“不小于”等数学术语，准确迅速地转化为数学符号．此类题是为学生以后列不等式解应用题做铺垫的，所以必须掌握好． 查看习题详情和答案>>