题目内容
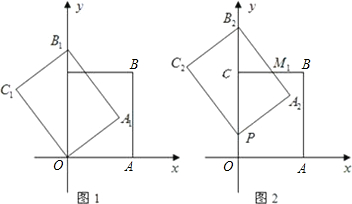
如图1,以矩形OABC的两边OA和OC所在的直线为x轴、y轴建立平面直角坐标系,A点的坐标为(3,0),C点的坐标为(0,4).将矩形OABC绕O点逆时针旋转,使B点落在y轴的正半轴上,旋转后的矩形为OA1B1C1,BC,A1B1相交于点M.(1)求点B1的坐标与线段B1C的长;
(2)将图1中的矩形OA1B1C1沿y轴向上平移,如图2,矩形PA2B2C2是平移过程中的某一位置,BC,A2B2相交于点M1,点P运动到C点停止.设点P运动的距离为x,矩形PA2B2C2与原矩形OABC重叠部分的面积为y,求y关于x的函数关系式,并写出x的取值范围;
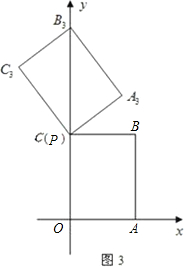
(3)如图3,当点P运动到点C时,平移后的矩形为PA3B3C3.请你思考如何通过图形变换使矩形PA3B3C3与原矩形OABC重合,请简述你的做法.
分析:(1)用勾股定理求矩形OABC的对角线OB长,得点B1的坐标;B1C=B1O-OC;
(2)求分段函数,以A2落在BC上的时刻为界,将函数分为两段,画出图形,分别求函数解析式;
(3)属于开放性问题,解法多种,主要是围绕旋转,平移轴对称解题.
(2)求分段函数,以A2落在BC上的时刻为界,将函数分为两段,画出图形,分别求函数解析式;
(3)属于开放性问题,解法多种,主要是围绕旋转,平移轴对称解题.
解答:解:(1)如图1,因为OB1=OB=
=5,
所以点B1的坐标为(0,5).
因为C(0,4),所以OC=4,
则B1C=OB1-OC=5-4=1.
(2)在矩形OA1B1C1沿y轴向上平移到P点与C点重合的过程中,点A1运动到矩形OABC的边BC上时,
重叠部分的面积为三角形PA2C的面积,A2C=
=
,又A2P=3,
根据勾股定理得:CP=
,即4-x=
求得P点移动的距离x=
.
当自变量x的取值范围为0≤x<
时,
如图2,由△B2CM1∽△B2A2P,
得CM1=
,此时,y=S△B2A2P-S△B2CM1=
×3×4-
×
(1+x),
即y=-
(x+1)2+6(或y=-
x2-
x+
).
当自变量x的取值范围为
≤x≤4时,
求得y=S△PCM1′=
(x-4)2(或y=
x2-
x+
).
(3)答案:
①把矩形PA3B3C3沿∠BPA3的角平分线所在直线对折.
②把矩形PA3B3C3绕C点顺时针旋转,使点A3与点B重合,再沿y轴向下平移4个单位长度.
③把矩形PA3B3C3绕C点顺时针旋转,使点A3与点B重合,再沿BC所在的直线对折.
④把矩形PA3B3C3沿y轴向下平移4个单位长度,再绕O点顺时针旋转,使点A3与点A重合.
提示:本问只要求整体图形的重合,不必要求图形原对应点的重合.
| 32+42 |
所以点B1的坐标为(0,5).
因为C(0,4),所以OC=4,
则B1C=OB1-OC=5-4=1.
(2)在矩形OA1B1C1沿y轴向上平移到P点与C点重合的过程中,点A1运动到矩形OABC的边BC上时,
重叠部分的面积为三角形PA2C的面积,A2C=
| 3×4 |
| 5 |
| 12 |
| 5 |
根据勾股定理得:CP=
| 9 |
| 5 |
| 9 |
| 5 |
求得P点移动的距离x=
| 11 |
| 5 |
当自变量x的取值范围为0≤x<
| 11 |
| 5 |
如图2,由△B2CM1∽△B2A2P,
得CM1=
| 3+3x |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3+3x |
| 4 |
即y=-
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 45 |
| 8 |
当自变量x的取值范围为
| 11 |
| 5 |
求得y=S△PCM1′=
| 2 |
| 3 |
| 2 |
| 3 |
| 16 |
| 3 |
| 32 |
| 3 |
(3)答案:
①把矩形PA3B3C3沿∠BPA3的角平分线所在直线对折.
②把矩形PA3B3C3绕C点顺时针旋转,使点A3与点B重合,再沿y轴向下平移4个单位长度.
③把矩形PA3B3C3绕C点顺时针旋转,使点A3与点B重合,再沿BC所在的直线对折.
④把矩形PA3B3C3沿y轴向下平移4个单位长度,再绕O点顺时针旋转,使点A3与点A重合.
提示:本问只要求整体图形的重合,不必要求图形原对应点的重合.
点评:本题主要考查图形的旋转、平移、折叠变换知识,是一道动态问题.

练习册系列答案
相关题目
 长线交于点E.
长线交于点E.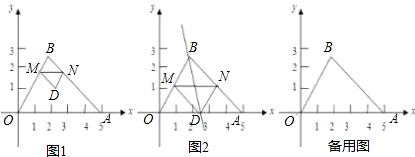
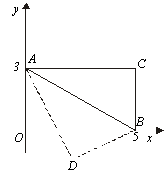
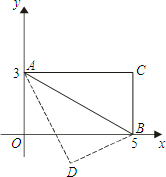 已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为( )
已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为( )