摘要:2.如图.抛物线与轴交于.两点.与轴交于点..则下列各式成立的是 A. B. C. D.
网址:http://m.1010jiajiao.com/timu3_id_442295[举报]
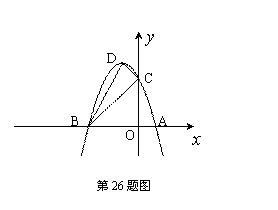
如图,抛物线与![]() 轴交于
轴交于![]() (
(![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() (
(![]() 设抛物线的顶点为
设抛物线的顶点为![]() .
.
(1)求该抛物线的解析式与顶点![]() 的坐标.
的坐标.
(2)试判断△![]() 的形状,并说明理由.
的形状,并说明理由.
(3)探究坐标轴上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似?
相似?
若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 |
查看习题详情和答案>>
如图,抛物线与![]() 轴交于
轴交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)两点,且
,0)两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 是方程
是方程![]() 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)点![]() 在(1)中抛物线上,点
在(1)中抛物线上,点![]() 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点![]() 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。

如图,抛物线与![]() 轴交于
轴交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)两点,且
,0)两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 是方程
是方程![]() 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)点![]() 在(1)中抛物线上,点
在(1)中抛物线上,点![]() 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点![]() 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
 |
查看习题详情和答案>>

 轴交于
轴交于 (2)点
(2)点 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以