摘要：源于课本的题目呈加强的趋势.03年.04年虽然对课本上的题目也有体现.但05年呈现出了加强的趋势 例13 一枝蜡烛长20厘米.点燃后每小时燃烧掉5厘米.则下列4幅图象中能较好刻画出这枝蜡烛点燃后剩下的长度h 与点燃时间t 之间的函数关系是 A． B． C． D． 本题是蜡烛燃烧中剩余高度与时间的函数.用函数图象来刻画．源于课本八年级下册35页第2题． 例14 若△ABC内切圆的切点将该圆圆周分为7:8:9三条弧.则△ABC的最小内角为 A．55° B．50° C．45° D． 30° 本题源于课本九年级下册63页第10题.是此题的简单改造． 例15 有一个抛物线形的拱形隧道.隧道的最大高度为6 m.跨度为8 m.把它放在如图所示的平面直角坐标系中．(1) 求这条抛物线所对应的函数关系式,(2) 若要在隧道壁上点P 安装一盏照明灯.灯离地面高4.5 m．求灯与点B的距离． 本题是抛物线型拱顶隧道的函数研究.源于课本九年级下册19页第5题． 例16 在△ABC中.AB = 2.AC = BC.CD⊥AB.垂足是D.△BCE与△BCD是关于BC成轴对称的.且恰好使A.C.E在一条直线上．求四边形BDCE的面积．本题源于九年级下册41页练习3.44页习题4.60页第4题． 因此提醒老师们复习时注意到课本上典型例习题的挖掘
网址：http://m.1010jiajiao.com/timu3_id_441023[举报]
在课外小组活动时，小慧拿来一道题（原问题）和小东、小明交流．
原问题：如图1，已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F．探究线段DF与EF的数量关系．
小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解．
小东同学说：我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60度．
小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况．
请你参考小慧同学的思路，探究并解决这三位同学提出的问题：
（1）写出原问题中DF与EF的数量关系；
（2）如图2，若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
（3）如图3，若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，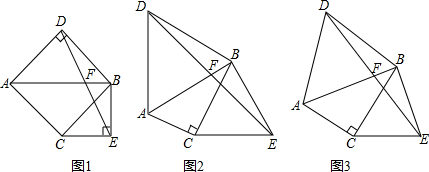
你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明．
查看习题详情和答案>>
原问题：如图1，已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F．探究线段DF与EF的数量关系．
小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解．
小东同学说：我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60度．
小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况．
请你参考小慧同学的思路，探究并解决这三位同学提出的问题：
（1）写出原问题中DF与EF的数量关系；
（2）如图2，若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
（3）如图3，若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，
你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明．
查看习题详情和答案>>
在课外小组活动时，小慧拿来一道题（原问题）和小东、小明交流．
原问题：如图1，已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F．探究线段DF与EF的数量关系．
小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解．
小东同学说：我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60度．
小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况．
请你参考小慧同学的思路，探究并解决这三位同学提出的问题：
（1）写出原问题中DF与EF的数量关系；
（2）如图2，若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
（3）如图3，若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明．
查看习题详情和答案>>
原问题：如图1，已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F．探究线段DF与EF的数量关系．
小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解．
小东同学说：我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60度．
小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况．
请你参考小慧同学的思路，探究并解决这三位同学提出的问题：
（1）写出原问题中DF与EF的数量关系；
（2）如图2，若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
（3）如图3，若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明．
查看习题详情和答案>>
在课外小组活动时，小慧拿来一道题（原问题）和小东、小明交流。
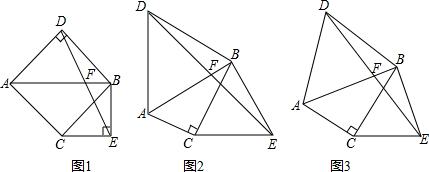
原问题：如图（1），已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F探究线段DF与EF的数量关系。
小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解；
小东同学说：我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60°；
小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况，请你参考小慧同学的思路，探究并解决这三位同学提出的问题：
原问题：如图（1），已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F探究线段DF与EF的数量关系。
小慧同学的思路是：过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解；
小东同学说：我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60°；
小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况，请你参考小慧同学的思路，探究并解决这三位同学提出的问题：
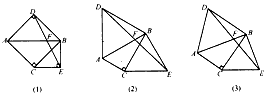
（1）写出原问题中DF与EF的数量关系；
（2）如图（2），若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
（3）如图（3），若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明。
查看习题详情和答案>>
（2）如图（2），若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
（3）如图（3），若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明。
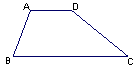
如图，小强家的一块四边形土地呈梯形
的形状，其中AD∥BC，小强家打算在这块地种植樱桃和杏，要使樱桃和杏的面积相等，请你设计一种方案，仅用一条直线，将梯形
的面积呈相等的两部分。
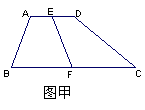
甲方案：如图甲所示，分别取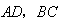
的中点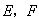
，连接EF，则四边形ABFE与四边形EFCD的面积相等。
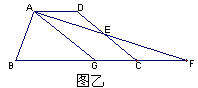
乙方案：如图乙，取DC中点E，连接AE并延续长，交BC的延长线与点F，取BF的中点G，连接AG，则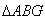
与四边形AGCD的面积相等；
（1）你认为谁的方案正确？请说明你的理由；
（2）你还有其他方案，可平分梯形ABCD的面积吗？
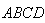的形状，其中AD∥BC，小强家打算在这块地种植樱桃和杏，要使樱桃和杏的面积相等，请你设计一种方案，仅用一条直线，将梯形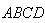的面积呈相等的两部分。甲方案：如图甲所示，分别取
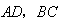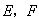的中点，连接EF，则四边形ABFE与四边形EFCD的面积相等。乙方案：如图乙，取DC中点E，连接AE并延续长，交BC的延长线与点F，取BF的中点G，连接AG，则
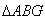与四边形AGCD的面积相等；（1）你认为谁的方案正确？请说明你的理由；
（2）你还有其他方案，可平分梯形ABCD的面积吗？
你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明．