摘要：如图,抛物线y=ax2+bx+c(a≠0)的图像与x轴的一个交点是.下列说法中不正确的是( ) A．抛物线的对称轴是x=1 B．抛物线的开口向下 C．抛物线与x轴的另一个交点是(2.0) D．当x=1时.y有最大值是3
网址：http://m.1010jiajiao.com/timu3_id_440802[举报]
如图，抛物线y=ax2+bx-3与x轴交于两点A（1，0）、B（3，0），与y轴交于点D．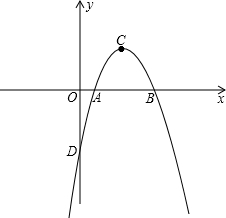
（1）求抛物线的解析式；
（2）在抛物线是否存在一点P，使得△BDP是以BD为斜边的直角三角形，若存在，请求出点P的坐标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，过M作MN⊥x轴于点N，使以A、M、N为顶点的三角形与△BCD相似？若存在，则求出点M的坐标；若不存在，请说明理由． 查看习题详情和答案>>
（1）求抛物线的解析式；
（2）在抛物线是否存在一点P，使得△BDP是以BD为斜边的直角三角形，若存在，请求出点P的坐标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，过M作MN⊥x轴于点N，使以A、M、N为顶点的三角形与△BCD相似？若存在，则求出点M的坐标；若不存在，请说明理由． 查看习题详情和答案>>
如图，抛物线y=ax2-4ax+c交x轴于A、B两点，交y轴于C点，点D（4，-3）在抛物
线上，且四边形ABDC的面积为18．
（1）求抛物线的函数关系式；
（2）若正比例函数y=kx的图象将四边形ABDC的面积分为1：2的两部分，求k的值；
（3）将△AOC沿x轴翻折得到△AOC′，问：是否存在这样的点P，以P为位似中心，将△AOC′放大为原来的两倍后得到△EPG（即△EPG∽△AOC′，且相似比为2），使得点E、G恰好在抛物线上？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由． 查看习题详情和答案>>
线上，且四边形ABDC的面积为18．（1）求抛物线的函数关系式；
（2）若正比例函数y=kx的图象将四边形ABDC的面积分为1：2的两部分，求k的值；
（3）将△AOC沿x轴翻折得到△AOC′，问：是否存在这样的点P，以P为位似中心，将△AOC′放大为原来的两倍后得到△EPG（即△EPG∽△AOC′，且相似比为2），使得点E、G恰好在抛物线上？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由． 查看习题详情和答案>>
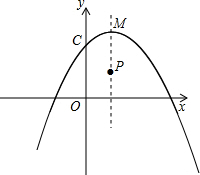如图，抛物线y=ax2+bx+c的顶点M的坐标是（1，3），且与y轴相交于点C（0，2），P（1，1）是抛物线对称轴上的一点．请回答下列问题：（1）写出抛物线的解析式
（2）点Q是抛物线上的一点，且使△CPQ的面积等于△CMP的面积，则所有满足条件的点Q的个数为：
R是小圆半径r的4倍．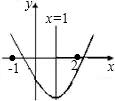
如图，抛物线y=ax2+bx+c的对称轴是x=1，下列结论：①b＜0；②（a+c）2＞b2；③2a+b-c＞0；④3b＜2c．其中正确的结论有