摘要：如图21.已知抛物线的图象与x轴交于A.C两点. (1)若抛物线关于x轴对称.求的解析式, (2)若点B是抛物线上一动点.以AC为对角线.A.B.C三点为顶点的平行四边形的第四个顶点记为D.求证:点D在上, (3)探索:当点B分别位于在x轴上.下两部分的图象上时.□ABCD的面积是否存在最大值或最小值?若存在.判断它是何种特殊平行四边形并求出它的面积,若不存在.请说明理由. 解:(1)设的解析式为y＝. ∵与x轴的交点A.顶点坐标是. 并且与关于x轴对称. ∴经过点A.顶点坐标是(0.4). ∴y＝. ∴0＝4a+4 得a＝-1. ∴的解析式为. (2)设B() ∵点B在上. ∴B() ∵四边形ABCD是平行四边形.A.C关于O对称. ∴B.D关于原点O对称. ∴D(). 将D()的坐标代入: 可知 左边＝右边. ∴点D在上. (3)设□ABCD的面积为S.则S＝2×. (I)当点B在x轴上方时.＞0. ∴.它是关于的正比例函数且S随的增大而增大. ∴S既无最大值也无最小值. (II)当点B在x轴下方时.-4≤＜0. ∴.它是关于的正比例函数且S随的增大而减小. ∴当＝-4时.S有最大值16.但它没有最小值. 此时B在y轴上.它的对称点D也在y轴上. ∴AC⊥BD. ∴□ABCD是菱形.此时.
网址：http://m.1010jiajiao.com/timu3_id_440801[举报]
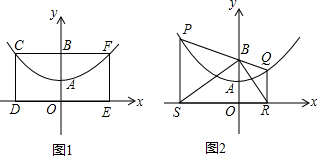
（2009•黔南州）如图1，已知抛物线的顶点为A（0，1），矩形CDEF的顶点C、F在抛物线上，D、E在x轴上，CF交y轴于点B，且其面积为8，F点的坐标为（2，2）．
（1）求此抛物线的解析式；
（2）如图2，若P点为抛物线上不同于A的一点，连结PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R．
①求证：PB=PS；
②试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似？若存在，请找出M点的位置；若不存在请说明理由．
查看习题详情和答案>>
（1）求此抛物线的解析式；
（2）如图2，若P点为抛物线上不同于A的一点，连结PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R．
①求证：PB=PS；
②试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似？若存在，请找出M点的位置；若不存在请说明理由．
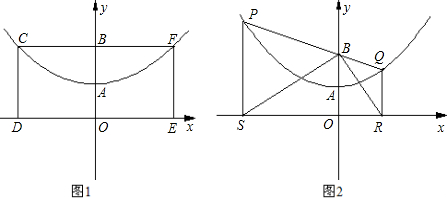
如图1，已知抛物线的顶点为A（0，1），矩形CDEF的顶点C、F在抛物线上，D、E在x轴上，CF交y轴于点B（0，2），且其面积为8．
（1）求此抛物线的解析式；
（2）如图2，若P点为抛物线上不同于A的一点，连接PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R．
①求证：PB=PS；
②判断△SBR的形状；
③试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似？若存在，请找出M点的位置；若不存在，请说明理由．
查看习题详情和答案>>
（1）求此抛物线的解析式；
（2）如图2，若P点为抛物线上不同于A的一点，连接PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R．
①求证：PB=PS；
②判断△SBR的形状；
③试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似？若存在，请找出M点的位置；若不存在，请说明理由．
查看习题详情和答案>>
如图1，已知抛物线的顶点为A（O，1），矩形CDEF的顶点C、F在抛物线上，D、E在x
轴上，CF交y轴于点B（0，2），且其面积为8．
（1）求此抛物线的解析式；
（2）如图2，若P点为抛物线上不同于A的一点，连接PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R．
①求证：PB=PS；
②判断△SBR的形状．
查看习题详情和答案>>
轴上，CF交y轴于点B（0，2），且其面积为8．（1）求此抛物线的解析式；
（2）如图2，若P点为抛物线上不同于A的一点，连接PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R．
①求证：PB=PS；
②判断△SBR的形状．
