题目内容
如图1,已知抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.

(1)求抛物线的解析式;
(2)连接OA,AB,如图2,在x轴下方的抛物线上是否存在点P,使得△OBP与△OAB相似?若存在,求出P点的坐标;若不存在,说明理由.

(1)求抛物线的解析式;
(2)连接OA,AB,如图2,在x轴下方的抛物线上是否存在点P,使得△OBP与△OAB相似?若存在,求出P点的坐标;若不存在,说明理由.
分析:(1)由题意可设抛物线的解析式为y=a(x-2)2+1,再根据抛物线过原点可求出a的值,故可得出抛物线的解析式;
(2)由抛物线的对称性可知:AO=AB,∠AOB=∠ABO,由△BOP与△AOB相似可知∠POB=∠BOA=∠BPO,设OP交抛物线的对称轴于C点,求出C点坐标及直线OP的解析式,把抛物线的解析式与直线OP的解析式组成方程组即可求出P点坐标,过P作PE⊥x轴,在Rt△BEP中利用勾股定理可求出BP的长,由PB≠OB可知∴△PBO与△BAO不相似,同理可说明在对称轴左边的抛物线上也不存在符合条件的P点.
(2)由抛物线的对称性可知:AO=AB,∠AOB=∠ABO,由△BOP与△AOB相似可知∠POB=∠BOA=∠BPO,设OP交抛物线的对称轴于C点,求出C点坐标及直线OP的解析式,把抛物线的解析式与直线OP的解析式组成方程组即可求出P点坐标,过P作PE⊥x轴,在Rt△BEP中利用勾股定理可求出BP的长,由PB≠OB可知∴△PBO与△BAO不相似,同理可说明在对称轴左边的抛物线上也不存在符合条件的P点.
解答: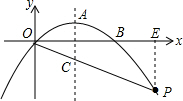 解:(1)由题意可设抛物线的解析式为y=a(x-2)2+1.
解:(1)由题意可设抛物线的解析式为y=a(x-2)2+1.
∵抛物线过原点,
∴0=a(0-2)2+1,
∴a=-
.
故抛物线的解析式为y=-
(x-2)2+1,即y=-
x2+x.
(2)如图,由抛物线的对称性可知:AO=AB,∠AOB=∠ABO.
∵△BOP与△AOB相似,
∴∠POB=∠BOA=∠BPO.
设OP交抛物线的对称轴于C点,
∴C(2,-1),
∴直线OP的解析式为y=-
x,
∵抛物线与直线OP有交点,
∴-
x=-
x2+x,
解得x1=0,x2=6.
∴P(6,-3).
过P作PE⊥x轴,
在Rt△BEP中,
∵BE=2,PE=3,
∴PB=
=
≠4.
∴PB≠OB.
∴∠BOP≠∠BPO.
∴△PBO与△BAO不相似,
同理可说明在对称轴左边的抛物线上也不存在符合条件的P点.
故在该抛物线上不存在点P,使得△OBP与△OAB相似.
 解:(1)由题意可设抛物线的解析式为y=a(x-2)2+1.
解:(1)由题意可设抛物线的解析式为y=a(x-2)2+1.∵抛物线过原点,
∴0=a(0-2)2+1,
∴a=-
| 1 |
| 4 |
故抛物线的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
(2)如图,由抛物线的对称性可知:AO=AB,∠AOB=∠ABO.
∵△BOP与△AOB相似,
∴∠POB=∠BOA=∠BPO.
设OP交抛物线的对称轴于C点,
∴C(2,-1),
∴直线OP的解析式为y=-
| 1 |
| 2 |
∵抛物线与直线OP有交点,
∴-
| 1 |
| 2 |
| 1 |
| 4 |
解得x1=0,x2=6.
∴P(6,-3).
过P作PE⊥x轴,
在Rt△BEP中,
∵BE=2,PE=3,
∴PB=
| 22+32 |
| 13 |
∴PB≠OB.
∴∠BOP≠∠BPO.
∴△PBO与△BAO不相似,
同理可说明在对称轴左边的抛物线上也不存在符合条件的P点.
故在该抛物线上不存在点P,使得△OBP与△OAB相似.
点评:本题考查的是二次函数综合题,此题涉及到用待定系数法求二次函数的解析式、相似三角形的性质、勾股定理等相关知识,难度适中.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
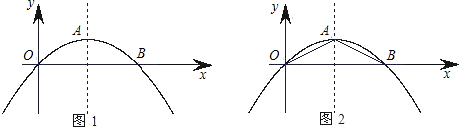

 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.