摘要：已知抛物线. (1) 求证此抛物线与x轴有两个不同的交点, (2) 若m是整数.抛物线与x轴交于整数点.求m的值, 的条件下.设抛物线的顶点为A.抛物线与x轴的两个交点中右侧交点为B. 若m为坐标轴上一点.且MA=MB.求点M的坐标. 解:(1)证明:令.则.因为=.所以此抛物线与x轴有两个不同的交点. (2)因为关于x的方程的根为.由m为整数.当为完全平方数时.此抛物线与x轴才有可能交于整数点.设(其中n为整数).则因为与的奇偶性相同. 所以或 解得 . 经过检验.当时.方程有整数根. 所以. (3)当m=2时.此二次函数解析式为 .则顶点坐标为. 抛物线与x轴的交点为.. 设抛物线的对称轴与x轴交于点.则. 在直角三角形中.由勾股定理.得. 由抛物线的对称性可得.. 又.即.所以△ABO为等腰直角三角形. 则. 所以为所求的点. 若满足条件的点在y轴上时.设坐标为. 过A作AN⊥y轴于N.连结..则.由勾股定理.有,. 即. 解得y=1. 所以为所求的点. 综上所述.满足条件的M点的坐标为.
网址：http://m.1010jiajiao.com/timu3_id_440790[举报]
已知抛物线
．
（1）求抛物线顶点M的坐标；
（2）若抛物线与x轴的交点分别为点A、B（点A在点B的左边），与y轴交于点C，点N为线段BM上的一点，过点N作x轴的垂线，垂足为点Q．当点N在线段BM上运动时（点N不与点B，点M重合），设NQ的长为t，四边形NQAC的面积为S，求S与t之间的函数关系式及自变量t的取值范围；
（3）在对称轴右侧的抛物线上是否存在点P，使△PAC为直角三角形?若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
查看习题详情和答案>>已知抛物线
．
（1）求抛物线顶点M的坐标；
（2）若抛物线与x轴的交点分别为点A、B（点A在点B的左边），与y轴交于点C，点N为线段BM上的一点，过点N作x轴的垂线，垂足为点Q．当点N在线段BM上运动时（点N不与点B，点M重合），设NQ的长为t，四边形NQAC的面积为S，求S与t之间的函数关系式及自变量t的取值范围；
（3）在对称轴右侧的抛物线上是否存在点P，使△PAC为直角三角形?若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
查看习题详情和答案>>已知抛物线y=mx2-(m+5)x+5.
(1)求证:它的图象与x轴必有交点,且过x轴上一定点;
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,0),且0<x1<x2,过(1) 中定点的直线L;y=x+k交y轴于点D,且AB=4,圆心在直线L上的⊙M为A、B两点,求抛物线和直线的关系式,弦AB与弧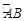
围成的弓形面积.
查看习题详情和答案>>
.
与x轴交于整数点，求m的值；
．
与x轴交于整数点，求m的值；