题目内容
(2005 北京东城)已知抛物线 .
.
(1)求证此抛物线与x轴有两个不同的交点;
(2)若m是整数,抛物线 与x轴交于整数点,求m的值;
与x轴交于整数点,求m的值;
(3)在(2)的条件下,设抛物线顶点为A,抛物线与x轴的两个交点中右侧交点为B.若M为坐标轴上一点,且MA=MB,求点M的坐标.
答案:略
解析:
提示:
解析:
|
解 (1)证明:令y=0,则 . .
因为 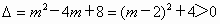 , ,
所以此抛物线与 x轴有两个不同的交点.(2) 解法一因为关于x的方程 由m为整数,当 设 所以[n+(m-2)][n-(m-2)]=4. 因为n+(m-2)与n-(m-2)的奇偶性相同, 所以 解得m=2. 经检验,当m=2时,关于x的方程 所以m=2. 解法二 设a是原方程的根,则a为整数,代入方程,得 a2-ma+m-2=0,解出
m、a都为整数,所以 故m=2. (3) 当m=2时,此二次函数解析式为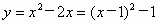 ,则顶点A的坐标为(1,-1).抛物线与x轴的交点为O(0,0)、B(2,0). ,则顶点A的坐标为(1,-1).抛物线与x轴的交点为O(0,0)、B(2,0).
如图所示,设抛物线的对称轴与 x轴交于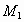 ,则 ,则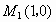 .在直角三角形 .在直角三角形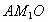 中,由勾股定理,得 中,由勾股定理,得 ,由抛物线的对称性可得, ,由抛物线的对称性可得,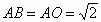 . .
又 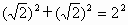 , ,
即  . .
所以△ ABO为等腰直角三角形.则  . .
所以 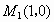 为所求的点. 为所求的点.
若满足条件的点 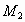 在y轴上时,设 在y轴上时,设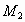 坐标为(0,y).过A作AN⊥y轴于N,连接 坐标为(0,y).过A作AN⊥y轴于N,连接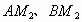 .则 .则 . .
由勾股定理,有 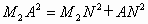 ; ;
即  .解得y=1. .解得y=1.
所以  为所求的点. 为所求的点.
综上所述满足条件的 M点的坐标为(1,0)或(0,1). |
提示:
|
点评 本题的第 (1)问考查判别式的应用.第(2)(3)问运用了分类的方法,其中隐含着探索性的数学思想,题目看似简单,实则综合性很强. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,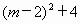 为完全平方数时,此抛物线与x轴才有可能交于整数点.
为完全平方数时,此抛物线与x轴才有可能交于整数点. (其中n为整数),
(其中n为整数), 或
或 .
.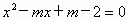 有整数根.
有整数根.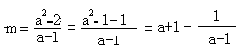

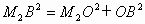
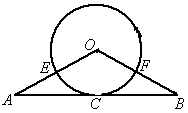
 ,求
,求 的长.
的长.