摘要:(1)建立如图所示的直角坐标系.求此抛物线的解析式, (2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地.已知甲地距此桥280 km.货车正以每小时40 km的速度开往乙地.当行驶1小时时.忽然接到紧急通知:前方连降暴雨.造成水位以每小时0.25 m的速度持续上涨(货车接到通知时水位在CD处.当水位达到桥拱最高点O时.禁止车辆通行).试问:如果货车按原来速度行驶.能否安全通过此桥?若能.请说明理由,若不能.要使货车安全通过此桥.速度应超过每小时多少千米?
网址:http://m.1010jiajiao.com/timu3_id_440668[举报]
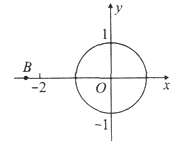
已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系,有一个正方形ABCD,顶点B的坐标为![]() ,顶点A在x轴上方,顶点D在⊙O上运动.
,顶点A在x轴上方,顶点D在⊙O上运动.
(1)求tan∠DBO的最大值;
(2)设正方形ABCD的面积为S,求S的取值范围;
(3)在顶点D运动的过程中,是否存在正方形ABCD的边CD与⊙O相功的情况?若存在,请确定此时DC与x轴的交点P的坐标;若不存在,请说明理由.
问题情境:
用同样大小的黑色棋子按如图所示的规律摆放,则第2012个图共有多少枚棋子?

建立模型:
有些规律问题可以借助函数思想来探讨,具体步骤:第一步,确定变量;第二步:在直角坐标系中画出函数图象;第三步:根据函数图象猜想并求出函数关系式;第四步:把另外的某一点代入验证,若成立,则用这个关系式去求解.
解决问题:
根据以上步骤,请你解答“问题情境”.

【解析】此题把规律问题借助函数思想来探讨,主要培养学生的应变能力和空间想象能力
查看习题详情和答案>>
按要求画图并填空:
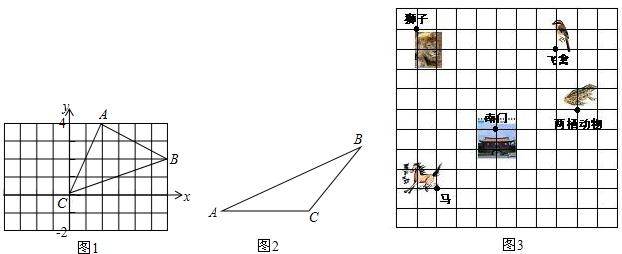
(1)△ABC在如图1所示的平面直角坐标系中,将其平移后得△A′B′C′,若B的对应点B′的坐标是(4,1).
①在图中画出△A′B′C′;
②此次平移可看作将△ABC向
③△A′B′C′的面积为
(2)已知:如图2,△ABC,请在图中作出它的角平分线BD,中线CE和BC边上的高AF.
(3)如图3,这是一个动物园游览示意图,试建立一个适当的平面直角坐标系描述这个动物园图中每个景点位置,(画出图形,并写出各景点的坐标).

查看习题详情和答案>>
(1)△ABC在如图1所示的平面直角坐标系中,将其平移后得△A′B′C′,若B的对应点B′的坐标是(4,1).
①在图中画出△A′B′C′;
②此次平移可看作将△ABC向
左
左
平移了2
2
个单位长度,再向下
下
平移了1
1
个单位长度得△A′B′C′;③△A′B′C′的面积为
10
10
.(2)已知:如图2,△ABC,请在图中作出它的角平分线BD,中线CE和BC边上的高AF.
(3)如图3,这是一个动物园游览示意图,试建立一个适当的平面直角坐标系描述这个动物园图中每个景点位置,(画出图形,并写出各景点的坐标).

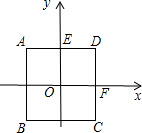 如图所示,以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系,若正方形的边长为4.
如图所示,以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系,若正方形的边长为4.