摘要:例1.如图6.四边形ABCD是矩形.O是它的中心.E.F是对角线AC上的点. (1)如果 .则ΔDEC≌ΔBFA(请你填上能使结论成立的一个条件), (2)证明你的结论. 知识点:考查了矩形的性质及三角形全等的判定. 精析:这是一道探索条件.补充条件的开放型试题.解决这类问题的方法是假设结论成立.逐步探索其成立的条件. 准确答案:解:(1)AE=CF(OE=OF,DE⊥AC,BF⊥AC,DE∥BF等等) (2)∵四边形ABCD是矩形.∴AB=CD.AB∥CD.∠DCE=∠BAF 又∵AE=CF.∴AC-AE=AC-CF.∴AF=CE.∴ΔDEC≌ΔBAF 中考对该知识点的要求:开放型试题重在开发思维.促进创新.提高数学素养.所以是近几年中考试题的热点考题. 目标达成: 9-1-1. 如图, E.F是□ABCD对角线BD上的两点.请你添加一个适当的条件: .使四边形AECF是平行四边形. 9-1-2.如图.在△ABC中.点D在AB上.点E在BC 上.BD=BE. (1)请你再添加一个条件.使得△BEA≌△BDC.并给出证明. 你添加的条件是: . 证明: (2)根据你添加的条件.再写出图中的一对全等三角形: . (只要求写出一对全等三角形.不再添加其他线段.不再标注或使用其他字母.不必写出证明过程) 9-1-3.如图19.在梯形ABCD中.AD∥BC.BD=CD.AB<CD且∠ABC为锐角.若AD=4.BC=12.E为BC上一点. 问:当CE分别为何值时.四边形ABED是等腰梯形?直角梯形? 请分别说明理由. 例2.己知点E.F在的边 AB 所在的直线上.且..FH.EG分别交边BC所在的直线于点H.G. ⑴如图l.如果点E.F在边AB上.那么, ⑵如图2.如果点E在边AB上.点F在AB的延长线上.那么线段EG.FH.AC的长度关系是 , ⑶如图3.如果点E在AB的反向延长线上.点F在AB的延长线上.那么线段EG.FH.AC的长度关系是 , 对⑴⑵⑶三种情况的结论.请任选一个给予证明. 知识点:考查了全等三角形.平行四边形的判定及性质以及平行线.分线段成比例或相似三角形的性质 精析:这是一道探索.确定结论的开放型试题.解决这类问题的方法是根据条件.结合已学的知识.数学思想方法.通过分析.归纳逐步得出结论.或通过观察.实验.猜想.论证的方法求解. 准确答案: (2)线段EG.FH.AC的长度的关系为:EG+FH=AC (3)线段 EG.FH.AC的长度的关系为:EG-FH=AC 证明(2):如图2.过点E作EP//BC交AC于P ∵EG//AC.∴四边形EPCG为平行四边形 ∴EG=PC ∵HF//EG//AC ∴. 又∵AE=BF ∴≌ ∴ ∴AC=PC+AP=EG+FH 即EG+FH=AC 中考对该知识点的要求:观察.实验.猜想.论证是科学思维方法.是新课标思维能力新添的内容.学习中应重视并应用. 目标达成: 9-2-1.如图1.AB是⊙O的直径.AC是弦.直线EF和⊙O相切于点C.AD⊥EF.垂足为D. (1)求证:∠DAC=∠BAC, (2)若把直线EF向上平行移动.如图2.EF交⊙O于G.C两点.若题中的其他条件不变.这时与∠DAC相等的角是哪一个?为什么? 9-2-2. 如图1.⊙O1与⊙O2都经过A.B两点.经过点A的直线CD与⊙O1交于点C.与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E.与⊙O2交于点F. (1)求证:CE∥DF, (2)在图1中.若CD和EF可以分别绕点A和点B转动.当点C与点E重合时.过点E作直线MN∥DF.试判断直线MN与⊙O1的位置关系.并证明你的结论. 9-2-3.己知:如图.E.F分别是□ABCD的AD.BC边上的点.且AE=CF. (1)求证:△ABE≌△CDF, (2)若M.N分别是BE.DF的中点.连结MF.EN. 试判断四边形MFNE是怎样的四边形.并证明你的结论. 9-2-4.如图.已知⊙O的弦AB垂直于直径CD.垂足为F.点E在AB上.且EA = EC. ⑴ 求证:AC 2 = AE·AB, ⑵ 延长EC到点P.连结PB.若PB = PE.试判断PB与⊙O的位置关系.并说明理由. 9-2-5.如图.⊙O1和⊙O2外切于点P.直线AB是两圆的外公切线.A,B为切点.试判断以线段AB为直径的圆与直线O1O2的位置关系.并说明理由. 例3.如图.直线CF垂直且平分AD于点E.四边形ADCB是菱形.BA的延长线交CF于点F.连接AC. (1) 图中有几对全等三角形.请把它们都写出来, (2)证明:△ABC是正三角形. 知识点:考查三角形全等的判定.垂直平分线的性质及菱形的性质及等边三角 形的判定等知识点. 精析:本题需学生根据给定的条件.通过观察.分析.探索多个不明确的结论.求解此类问题时.切勿凭空乱想.应仔细对照条件.观察图形特征.联想已学知识.方法或已解决过的问题.全方位的.多角度地作全面分析. 准确答案:(1)图中有四对全等三角形.分别为△ABC≌△CDA.△AEF≌△DEC.△DEC≌△AEC.△AEF≌△AEC. (2)证明: ∵CF垂直平分AD. ∴AC=CD 又∵四边形ABCD是菱形. ∴AB=BC=CD=DA ∴AB=BC=AC ∴△ABC为正三角形. 中考对该考点的要求:这类试题因为对学生的观察能力.分析问题和解决问题的能力有一定的要求.所以最近几年中考试题的命题热点. 目标达成: 9-3-1已知:如图.在△ABC中.点D.E分贝在边AB.AC上.连结DE并延长交BC的延长线于点F.连结DC.BE.若∠BDE+∠BCE=180°. (1)写出图中三对相似三角形(注意:不得添加字母和线), (2)请在你所找出的相似三角形中选取一对.说明它们相似的理由. 9-3-2.如图.已知E.F是□ABCD的边BA.DC延长线上的点.且AE=CF.线段EF分别交AD.BC于点M.N. 请你在图中找出一对全等三角形并加以证明. 解:我选择证明△ ≌△ . 9-3-3.如图.将等腰直角三角形ABC的直角顶点置于直线上.且过A.B两点分别作直线的垂线.垂足分别为D.E.请你仔细观察后.在图中找出一对全等三角形.并写出证明它们全等的过程. 9-3-4.如图.四边形ABCD中.AC垂直平分BD于点O. (1) 图中有多少对全等三角形?请把它们都写出来, 中的一对全等三角形加以证明. 9-3-5.如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD.CF相交于点H,它们的延长线分别交GE于点E.G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明. 能力提高: 9-1.已知△ABC.分别以AB.BC. CA为边向形外作等边三角形ABD.等边三角形BCE.等边三角形ACF. (1) 如图1.当△ABC是等边三角形时.请你写出满足图中条件.四个成立的结论, (2) 如图2.当△ABC中只有∠ACB=60°时.请你证明S△ABC与S△ABD的和等于S△BCE与S△ACF的和. 9-2.如图.给出五个等量关系:①AD=BC.②AC=BD.③CE=DE.④∠D=∠C. ⑤∠DAB=∠CBA.请你以其中两个为条件.另三个中的一个为结论.写出一个正确命题.并加以证明. 9-3.将两块含30°角且大小相同的直角三角板如图1摆放. (1)将图1中△绕点C顺时针旋转45°得图2.点与AB的交点. 求证:, (2)将图2中△绕点C顺时针旋转30°到△.点与AB的交点.线段之间存在一个确定的等量关系.请你写出这个关系式并说明理由, (3)将图3中线段绕点C顺时针旋转60°到.连结.求证:⊥AB. 9-4.如图.梯形ABCD中.AD∥BC.AB=DC.P为梯形ABCD外一点.PA.PD分别交线段BC于点E.F.且PA=PD. (1)写出图中三对你认为全等的三角形, 中写出的全等三角形中的任意一对进行证明. 9-5.已知任意四边形ABCD.且线段AB.BC.CD.DA.AC.BD的中点分别是E.F.G.H.P.Q. (1)若四边形ABCD如图①.判断下列结论是否正确(正确的在括号里填“√ .错误的在括号里填“× ). 甲:顺次连接EF.FG.GH.HE一定得到平行四边形,( ) 乙:顺次连接EQ.QG.GP.PE一定得到平行四边形.( ) (2)请选择甲.乙中的一个.证明你对它的判断. (3)若四边形ABCD如图②.请你判断(1)中的两个结论是否成立? 9-6.如图.在□ABCD中.点E.F在BD上.且BF=DE. ⑴.写出图中所有你认为全等的三角形, ⑵.延长AE交BC的延长线于G.延长CF交DA的延长线于H.证明四边形AGCH是平行四边形. 9-7.如图.在△ABC中.AB=AC.AD⊥BC.D为垂足.由以上两个条件可得 . 9-8.如图11.AC是平行四边形ABCD的对角线. (1)用直尺和圆规作AC的垂直平分线和边AD.BC分别相交于点E.F.垂足为O.连结AF.CE(保留作图痕迹.不写作法) (2)判断四边形AFCE是否为菱形.并说明理由. 9-9.在某数学小组的活动中.组长为大家出了一道函数题:这是一个反比例函数.并且y随x的增大而减小.请你写山一个符合条件的函数表达式 . 9-10.如图.在等腰梯形ABCD中.AD//BC.M.N分别为AD.BC的中点.E.F分别是BM.CM的中点. (1)求证:, (2)四边形MENF是什么图形?请证明你的结论, (3)若四边形MENF是正方形.则梯形的高与底边BC有何数量关系?并请说明理由. 9-11.在平面内.如果一个图形绕一个定点旋转一定的角度后能与自身重合.那么就称这个图形是旋转对称图形.转动的这个角称为这个图形的一个旋转角.例如:正方形绕着它的对角线的交点旋转90°后能与自身重合.所以正方形是旋转对称图形.它有一个旋转角为90°. (1) 判断下列命题的真假(在相应的括号内填上“真 或“假 ). ①等腰梯形是旋转对称图形.它有一个旋转角为180°. ② 矩形是旋转对称图形.它有一个旋转角为180° (2)填空:下列图形中.是旋转对称图形.且有一个旋转角为120°的是 (写出所有正确结论的序号):①正三角形,②正方形,③正六边形,④正八边形 . (3)写出两个多边形.它们都是旋转对图形.都有一个旋转角为72°.并且分别满足下列条件 ①是轴对称图形.但不是中心对称图形: ②既是轴对称图形.又是中心对称图形: 9-12.如图.在锐角△ABC中.BA=BC.点O是边AB上的一个动点.以O为圆心.OA为半径的圆交边AC于点M.过点M作⊙O的切线MN交BC于点N. (1)当OA=OB时.求证:MN⊥BC, (2)分别判断OA<OB.OA>OB时.上述结论是否成立. 请选择一种情况.说明理由. 9-13.三个全等的菱形ABGH.BCFG.CDEF拼成平行四边形ADEH.连接AE与BG.CF分别交于P.Q. (1) 若AB=6.求线段BP的长, (2) 观察图形.是否有三角形与ΔACQ全等?并证明你的结论. 9-14.如图.AB是⊙O的直径.CB.CE分别切⊙O于点B.D. CE与BA的延长线交于点E.连结OC.OD. (1)求证:△OBC≌△ODC, (2)已知DE=a.AE=b.BC=c.请你思考后. 选用以上适当的数.设计出计算⊙O 半径r的一种方案: ①你选用的已知数是 , ②写出求解过程. 9-15.如图5,AB为圆O的直径,C为圆O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E. (1)判定直线DE与圆O的位置关系.并说明你的理由, (2)求证:AC2=AD∙AB, (3)以下两个问题任选一题做答 ① 若CF⊥AB于点F,试讨论线段CF.CE和DE三者的数量关系; ②若EC=5,EB=5,求图中阴影部分的面积. 图5 9-16.如图1:⊙O的直径为AB.过半径OA的中点G作弦CE⊥AB.在上取一点D.分别作直线CD.ED交直线AB于点F.M. (1)求∠COA和∠FDM的度数, (2)求证:△FDM∽△COM, (3)如图2:若将垂足G改取为半径OB上任意一点.点D改取在上.仍作直线CD.ED.分别交直线AB于点F.M.试判断:此时是否仍有△FDM∽△COM?证明你的结论. 9-2-17.已知:如图.直线交轴于.交轴于.⊙与轴相切于O点.交直线于P点.以为圆心P为半径的圆交轴于A.B两点.PB交⊙于点F.⊙的弦BE=BO.EF的延长线交AB于D.连结PA.PO. (1)求证:, (2)求证:EF是⊙的切线, (3)的延长线交⊙于C点.若G为BC上一动点.以为直径作⊙交于点M.交于N.下列结论①为定值,②线段MN的长度不变.只有一个是正确的.请你判断出正确的结论.并证明正确的结论.以及求出它的值. 9-1-1.略 9-1-2.添加条件例举:BA=BC,∠AEB=∠CDB,∠BAC=∠BCA,AE⊥BC. CD⊥AB等. 证明例举(以添加条件∠AEB=∠CDB为例): ∵ ∠AEB=∠CDB.BE=BD.∠B=∠B. ∴ △BEA≌△BDC. 另一对全等三角形是:△ADF≌△CEF或△AEC≌△CDA. 9-1-3.(1)当CE=4时.四边形ABED是等腰梯形. 理由如下: 在BC上截取CE=AD.连结DE.AE. ∵AD∥BC.∴四边形AECD是平行四边形.∴AE=CD=BD. ∵BE=12-4=8>4.即BE>AD.∴AB不平行于DE. ∴四边形ABED是梯形. ∵AE∥CD.CD=BD. ∴∠AEB=∠C=∠DBC. 在△ABE和△DEB中. ∴△ABE≌△DEB (SAS).∴AB=DE. ∴四边形ABED是等腰梯形. (也可不作辅助线.通过证明△ABD≌EDC而得AB=DE) (2)当C=6时.四边形ABD是直角梯形. 理由如下: 在BC上取一点.使C=B==6.连结D. ∵BD=CD ∴D⊥BC 又∵B≠AD.AD∥B. ∴AB不平行于D ∴四边形ABD是直角梯形. 9-2-1. 9-2-2. 9-2-3. 9-2-4.⑴连结BC 提示:可证△AEC∽△ACB 所以得.即AC2=AB·AE ⑵PB与⊙O相切 连结OB.∵PB=PE ∴∠PBE=∠PEB ∵∠1=∠2=∠3.∴∠PEB=∠1+∠3=2∠1 而∠PBE=∠2+∠PBC.∴∠OBC=∠OCB 而Rt△BCF中.∠OCB=90°-∠2=90°-∠1 ∴∠OBC=90°-∠1 ∴∠OBP=∠OBC+∠PBC=∠1+=90° ∴PB⊥OB.即PB为⊙O的切线. 9-2-5.解:直线O1O2与以线段AB为直径的圆相切. 理由如下: 过P作⊙01.⊙02的公切线PM交AB于点M.则 AM=MB=MP.O1O2⊥MP. ∴M点为以线段AB为直径的圆的圆心.且点P在⊙M上. ∵⊙01和⊙O2外切于点P. ∴直线O102过点P. ∴直线01O2与以线段AB为直径的圆相切. 9-3-1..解:(1)△ADE∽△ACB.△ECF∽△BDF.△FDC∽△FBE. (2)略. 9-3-2..解法一:我选择证明△EBN≌△FDM 证明:□ABCD中.AB∥CD.ÐB=ÐD.AB=CD ∴ÐE=ÐF 又∵AE=CF ∴BE=DF ∴△EBN≌△FDM 解法二:我选择证明△EAM≌△FCN 证明:□ABCD中.AB∥CD.ÐDAB=ÐBCD ∴ÐE=ÐF .ÐEAM=ÐFCN 又∵AE=CF ∴BE=DF ∴△EBN≌△FDM 9-3-3.△ACD≌△CBE 证:由题意知∠CAD+∠ACD=90°.∠ACD+∠BCE=90° ∴∠CAD=∠BCE 又∠ADC=∠CEB=90°.AC=CB ∴△ACD≌△CBE 9-3-4.解:(1)图中有三对全等三角形:△AOB≌△AOD. △COB≌△COD.△ABC≌△ADC. (2) 证明△ABC≌△ADC. 9-3-5.解:△BCF≌△CBD. △BHF≌△CHD. △BDA≌△CFA. 证明△BCF≌△CBD. ∵AB=AC. ∴∠ABC=∠ACB. - ∵BD.CF是角平分线. ∴∠BCF=∠ACB.∠CBD=∠ABC. ∴∠BCF=∠CBD. 又BC=CB. ∴△BCF≌△CBD. 9-1.1.解:(1)略. (2)解法一:过A作AM∥FC交BC于M.连结DM.EM. 因为∠ACB=60°.∠CAF=60°.所以∠ACB=∠CAF. 所以AF∥MC.所以四边形AMCF是平行四边形. 又因为FA=FC. 所以□AMCF是菱形. 所以AC=CM=AM.且∠MAC=60°. 在△BAC与△EMC中. CA=CM.∠ACB=∠MCE.CB=CE, 所以△BAC≌△EMC. 所以DM=BC. 则DM=EB.DB=EM. 所以四边形DBEM是平行四边形. 所以S△BDM+ S△DAM+ S△MAC= S△BEM+ S△EMC+ S△ACF. 即S△ABC+S△ABD=S△BCE+S△ACF. 9-2.①AD=BC.②AC=BD, 9-3.(1)证明:过点作CA的垂线.垂足为D 易知:△CD为等腰直角三角形 △DA是直角三角形.且∠A=30°. 所以 故 . (2)解: 过点作C的垂线.垂足为E.易知:△E为等腰直角三角形(其中∠2=∠A+∠CA=45°) △CE是直角三角形.且∠1=30°.所以 故 (3)证明:将图3中线段绕点C顺时针旋转60°到.易证: △≌△.于是∠=∠=45°. 故⊥AB. 9-4.①△ABP≌△DCP,②△ABE≌△DCF,③△BEP≌△CFP,④△BFP≌△CEP, (2)以△ABP≌△DCP全等为例: 证明:∵AD∥BC.AB=DC. ∴梯形ABCD为等腰梯形.∴∠BAD=∠CDA. 又∵PA=PD.∴∠PAD=∠PDA.∴∠BAP=∠CDP. 在△ABP和△DCP中. ∵.∴△ABP≌△DCP. 9-5.(1)甲 √ 乙 × 中对甲的判断: 连接EF.FG.GH.HE. ∵E.F分别是AB.BC的中点.∴EF是△ABC的中位线. ∴EF∥AC .EF=AC. 同理.HG∥AC .HG=AC. ∴EF∥HG.EF=HG.∴四边形EFGH是平行四边形. 9-6..⑴.△ABE≌△CDF.△AED≌△CFB.△ABD≌△CDB, ⑵.∵BF=DE.∴BF+FE=DE+FE.即BE=DE. ∵四边形ABCD是平行四边形.∴AB∥CD. ∴∠ABD=∠CDB. 在△ABE和△CDF中: ∴△ABE≌△CDF.∴∠AEB=∠CFD. ∴HC∥CG.∴四边形AGCH为平行四边形. 9-7. 9-8. 9-9.答案不惟一.例如.写出的关系式只要满足x·y值为正数即可. 9-10.(1)证明:ABCD为等腰梯形 .. (2)四边形MENF是菱形 (3)梯形的高等于底边BC的一半.连结MN 9-11.①.③,(3)①如正五边形.正十五边形,②如正十边形.正二十边形 9-12. 5. 9-13.(1) ∽ΔADE (2)图中的ΔEGP与ΔACQ全等- 证明:ABGH.BCFG.CDEF是全等的菱形 既AC=EG AD//HE ΔEGP≌ΔACQ 9-14.(1)证明:∵CD.CB是⊙O的切线.∴∠ODC=∠OBC=90°. OD=OB.OC= OC. ∴△OBC≌△ODC(HL), (2)①选择a.b.c. ②若选择a.b:由切割线定理:a2=b .得r=. 若选择a.b.c: 方法一:在Rt△EBC中.由勾股定理:2+c2=(a+c)2.得r=. 方法二:Rt△ODE∽Rt△CBE..得r=. 方法三:连结AD.可证:AD//OC..得r=. 若选择a.c:需综合运用以上的多种方法.得r=. 若选择b.c.则有关系式2r3+br2-bc2=0. 9-15.(1) DE是⊙O的切线. 提示: 连接OC (2) ∵AB为⊙O的直径 ∴∠ACB=900 ∵AD⊥DE ∠ADC=900 ∴ ∠ACB= ∠ADC 又∠DAC=∠CAB ∴⊿DAC∽⊿CAB ∴AC2=AD∙AB (3)①CF+CE=DE AC是∠DAB的平分线,且CD⊥AD.CF⊥AF, 则CF=CD 而DC+CE=DE 故CF+CE=DE ②∵DE是⊙O的切线 ∴ ∠BCE= ∠CAB ∠CEB公用 ∴⊿BCE∽⊿CAE ∴ ∴AE=15 AB=10 即CA=BC 则在Rt⊿ABC中,由CA2+BC2=AB2 解得 BC=5, CA=5.故图中阴影部分的面积为 - 9-16.解 ∠FDM=1800-∠CDE=1200 (2)证明: ∵∠COM=1800-∠COA=1200 ∴∠COM=∠FDM 在Rt△CGM和Rt△EGM中 ∵ ∴Rt△CGM≌Rt△EGM ∴∠GMC=∠GME 又∠DMF=∠GME ∴∠OMC=∠DMF ∴△FDM∽△COM (3)解:结论仍成立. ∵∠FDM=1800-∠CDE ∴∠CDE的度数=弧CAE的度数=的度数=∠COA的度数 ∴∠FDM=1800-∠COA=∠COM ∵AB为直径.CE⊥AB ∴在Rt△CGM和Rt△EGM中 ∵ ∴Rt△CGM≌Rt△EGM ∴∠GMC=∠GME ∴△FDM∽△COM 9-17.1. 证明:(1)连结. ∵. ∴, , ∴. ∴, 得.∴. 又AB为直径.∴, ∴. (2)延长ED交⊙于点H.连结PE. BO为切线.∴. 又∵BE=BO.∴.而,∴∽, ∴, ∴BE=BH, 有. 又由(1)知.∴.∴EF为⊙的切线. (3)MN的长度不变. 过N作⊙的直径NK.连结MK. 则.且.又NK=. ∴≌.∴MN=ED.而..∴=5. ∴. AB=16.且OD=.∴AD=7.BD=9. .∴. 故MN的长度不会发生变化.其长度为.
网址:http://m.1010jiajiao.com/timu3_id_440519[举报]
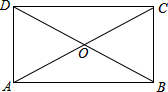 如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为
如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为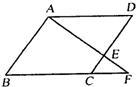 7、如图在平行四边形ABCD中,点E为边CD上的一点,AE的延长线交BC的延长线于点F,请你写出图中的一对相似三角形:
7、如图在平行四边形ABCD中,点E为边CD上的一点,AE的延长线交BC的延长线于点F,请你写出图中的一对相似三角形: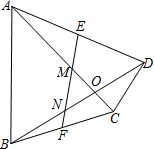 如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.
如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.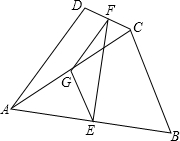 如图:在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点.
如图:在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点. 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )