题目内容
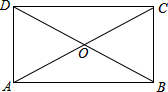 如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为
如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为分析:作DE⊥AC于E,由等边三角形的性质就可以求出△AOD的面积,在根据平行四边形的对角线分的四个三角形的面积相等就可以求出结论.
解答: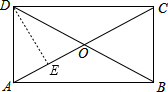 解:作DE⊥AC于E,
解:作DE⊥AC于E,
∴∠AED=90°.
∵△AOD是正三角形,
∴AD=DO=AO,AO=EO=
AO,∠ADO=∠DAO=60°,
∴∠ADE=30°.
∵AD=4,
∴AE=2.
在Rt△ADE中,由勾股定理,得
DE=2
,
∴S△AOD=
×4×2
=4
.
∵四边形ABCD是平行四边,
∴S△AOD=S△DOC=S△BOC=S△AOB,
∴平行四边形ABCD的面积=4×4
=16
.
故答案为:16
.
 解:作DE⊥AC于E,
解:作DE⊥AC于E,∴∠AED=90°.
∵△AOD是正三角形,
∴AD=DO=AO,AO=EO=
| 1 |
| 2 |
∴∠ADE=30°.
∵AD=4,
∴AE=2.
在Rt△ADE中,由勾股定理,得
DE=2
| 3 |
∴S△AOD=
| 1 |
| 2 |
| 3 |
| 3 |
∵四边形ABCD是平行四边,
∴S△AOD=S△DOC=S△BOC=S△AOB,
∴平行四边形ABCD的面积=4×4
| 3 |
| 3 |
故答案为:16
| 3 |
点评:本题考查了平行四边形的性质的运用,等边三角形的性质的运用,勾股定理的性质的运用,解答时运用勾股定理求出△AOD的面积是关键.

练习册系列答案
相关题目
 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB. 10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是

 如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是
如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为