摘要: 如图所示.平行四边形纸条ABCD中.E.F分别是边AD.BC的中点.张老师请同学们将纸条的下半部分平行四边形ABFE沿EF翻折.得到一个V字形图案. (1)请你在原图中画出翻折后的图形平行四边形A B FE,(用尺规作图.不写画法.保留作图痕迹) (2)已知的大小.
网址:http://m.1010jiajiao.com/timu3_id_440301[举报]
如图①,将四边形纸片ABCD沿两组对边中点连线剪切为四部分,将这四部分镶嵌可得到如图②所示的四边形O1O2O3O4.
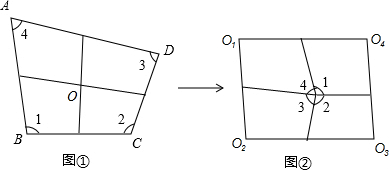
(1)试判断四边形O1O2O3O4的形状,并证明.
(2)若要镶嵌后的平行四边形O1O2O3O4为矩形,则四边形ABCD需要满足什么条件,并证明. 查看习题详情和答案>>

(1)试判断四边形O1O2O3O4的形状,并证明.
(2)若要镶嵌后的平行四边形O1O2O3O4为矩形,则四边形ABCD需要满足什么条件,并证明. 查看习题详情和答案>>
图1是两个正方形纸片ABCD和CEFG叠放在一起,分别以BC边所在直线和BC边的中垂线为坐标轴建立如图所示的坐标系,其中B(-2,0),E(2,
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1,
(1)在图2中求点E1的坐标,并直接写出点E1与直线L的位置关系.
(2)利用(1)的结论,将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移,平移后的正方形CE1F1G1设为正方形PQRH(图3),当点R移动到点A停止,设正方形PQRH移动的时间为t秒,正方形PQRH与正方形ABCD重叠部分的面积为S,请直接写出S与t之间的函数解析式,并写出函数自变量t的取值范围.
(3)在(2)的条件下,如果S=1时,过BP的直线为m,M点为直线m上的动点,N为直线L上的动点,那么是否存在平行四边形MNBC,如果存在,请求出M点的坐标,如果不存在,请说明理由.

查看习题详情和答案>>
| 2 |
(1)在图2中求点E1的坐标,并直接写出点E1与直线L的位置关系.
(2)利用(1)的结论,将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移,平移后的正方形CE1F1G1设为正方形PQRH(图3),当点R移动到点A停止,设正方形PQRH移动的时间为t秒,正方形PQRH与正方形ABCD重叠部分的面积为S,请直接写出S与t之间的函数解析式,并写出函数自变量t的取值范围.
(3)在(2)的条件下,如果S=1时,过BP的直线为m,M点为直线m上的动点,N为直线L上的动点,那么是否存在平行四边形MNBC,如果存在,请求出M点的坐标,如果不存在,请说明理由.

图1是两个正方形纸片ABCD和CEFG叠放在一起,分别以BC边所在直线和BC边的中垂线为坐标轴建立如图所示的坐标系,其中B(﹣2,0),E(2,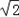 ),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
(1)在图2中求点E1的坐标,并直接写出点E1与直线L的位置关系.
(2)利用(1)的结论,将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移,平移后的正方形CE1F1G1设为正方形PQRH(图3),当点R移动到点A停止,设正方形PQRH移动的时间为t秒,正方形PQRH与正方形ABCD重叠部分的面积为S,请直接写出S与t之间的函数解析式,并写出函数自变量t的取值范围.
(3)在(2)的条件下,如果S=1时,过BP的直线为m,M点为直线m上的动点,N为直线L上的动点,那么是否存在平行四边形MNBC,如果存在,请求出M点的坐标,如果不存在,请说明理由.
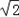 ),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.(1)在图2中求点E1的坐标,并直接写出点E1与直线L的位置关系.
(2)利用(1)的结论,将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移,平移后的正方形CE1F1G1设为正方形PQRH(图3),当点R移动到点A停止,设正方形PQRH移动的时间为t秒,正方形PQRH与正方形ABCD重叠部分的面积为S,请直接写出S与t之间的函数解析式,并写出函数自变量t的取值范围.
(3)在(2)的条件下,如果S=1时,过BP的直线为m,M点为直线m上的动点,N为直线L上的动点,那么是否存在平行四边形MNBC,如果存在,请求出M点的坐标,如果不存在,请说明理由.


