题目内容
如图①,将四边形纸片ABCD沿两组对边中点连线剪切为四部分,将这四部分镶嵌可得到如图②所示的四边形O1O2O3O4.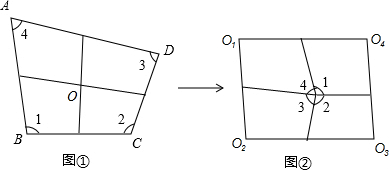
(1)试判断四边形O1O2O3O4的形状,并证明.
(2)若要镶嵌后的平行四边形O1O2O3O4为矩形,则四边形ABCD需要满足什么条件,并证明.
分析:(1)利用平行四边形的判定方法得出即可;
(2)首先认真读题,理解题意.密铺后的平行四边形成为矩形,必须四个内角均为直角,据此需要判定中点四边形EFGH为菱形,进而由中位线定理判定四边形ABCD的对角线垂直.
(2)首先认真读题,理解题意.密铺后的平行四边形成为矩形,必须四个内角均为直角,据此需要判定中点四边形EFGH为菱形,进而由中位线定理判定四边形ABCD的对角线垂直.
解答: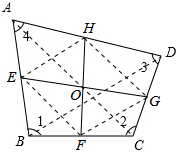 解:(1)平行四边形,
解:(1)平行四边形,
理由:∵将四边形纸片ABCD沿两组对边中点连线剪切为四部分,将这四部分镶嵌可得到如图②所示的四边形O1O2O3O4,
∴∠O1=∠O3,∠O2=∠O4,
∴四边形O1O2O3O4是平行四边形;
(2)对角线AC=BD时,密铺后的平行四边形为矩形.
理由:根据密铺后的平行四边形成为矩形,必须四个内角均为直角.
如解答图所示,连接EF、FG、GH、HE,设EG与HF交于点O,
连接AC、BD,由中位线定理得:EF∥AC∥GH,且EF=GH=
AC,
EH∥BD∥FG,且EH=FG=
BD,
∵AC=BD,
∴中点四边形EFGH为菱形,
∴EG⊥HF,
故要镶嵌后的平行四边形O1O2O3O4为矩形,则四边形ABCD需要满足的条件为AC=BD.
 解:(1)平行四边形,
解:(1)平行四边形,理由:∵将四边形纸片ABCD沿两组对边中点连线剪切为四部分,将这四部分镶嵌可得到如图②所示的四边形O1O2O3O4,
∴∠O1=∠O3,∠O2=∠O4,
∴四边形O1O2O3O4是平行四边形;
(2)对角线AC=BD时,密铺后的平行四边形为矩形.
理由:根据密铺后的平行四边形成为矩形,必须四个内角均为直角.
如解答图所示,连接EF、FG、GH、HE,设EG与HF交于点O,
连接AC、BD,由中位线定理得:EF∥AC∥GH,且EF=GH=
| 1 |
| 2 |
EH∥BD∥FG,且EH=FG=
| 1 |
| 2 |
∵AC=BD,
∴中点四边形EFGH为菱形,
∴EG⊥HF,
故要镶嵌后的平行四边形O1O2O3O4为矩形,则四边形ABCD需要满足的条件为AC=BD.
点评:本题考查图形剪拼与中点四边形.解题关键是理解三角形中位线的性质,熟练应用矩形、菱形等特殊四边形的判定与性质.

练习册系列答案
相关题目
 24、如图,有一四边形纸片ABCD,AB∥CD,AD∥BC,∠A=60°,将纸片分别沿折痕MN、PQ折叠,使点A与AB边上的点E重合,点C与CD边上的点F重合,EG平分∠MEB交CD于G,FH平分∠PFD交AB于H.试说明:
24、如图,有一四边形纸片ABCD,AB∥CD,AD∥BC,∠A=60°,将纸片分别沿折痕MN、PQ折叠,使点A与AB边上的点E重合,点C与CD边上的点F重合,EG平分∠MEB交CD于G,FH平分∠PFD交AB于H.试说明: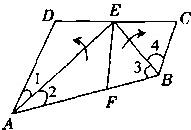 17、如图,已知四边形纸片ABCD中,AD∥BC,将∠ABC、∠DAB分别对折,如果两条折痕恰好相交于DC上一点E,你能获得哪些结论?
17、如图,已知四边形纸片ABCD中,AD∥BC,将∠ABC、∠DAB分别对折,如果两条折痕恰好相交于DC上一点E,你能获得哪些结论? (2012•河北区三模)如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号
(2012•河北区三模)如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号

