摘要:解:(1)设..由题设可求得C点的坐标为(0.c).且. 由S△AOC- S△BOC=OA·OB得: 2分 得: 3分 得:b=–2 4分 (2)设抛物线的对称轴与轴交于点M.与△PAB的外接圆交于点N. ∵tan∠CAB=, ∴OA=2·OC=2c, ∴A点的坐标为 5分 ∵A点在抛物线上.∴ 6分 又.为方程的两根. ∴.即: 7分 ∴B点的坐标为(.0) ∴顶点P的坐标为(-.) 8分 由相交弦定理得:AM.BM=PM.MN 又∵ ∴AM=BM=, ∴ 10分 ∴. ∴所求抛物线的函数解析式是: 11分
网址:http://m.1010jiajiao.com/timu3_id_440256[举报]
当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1…(1)
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x0,y0),则: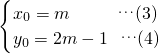
当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,将(3)代入(4)
得:y0=2x0-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是______,其中运用的公式是______.由(3)、(4)得到(5)所用的数学方法是______.
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2).
查看习题详情和答案>>
阅读材料:当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1…(1)
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x0,y0),则:
当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,将(3)代入(4)
得:y0=2x0-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是 ,其中运用的公式是 .由(3)、(4)得到(5)所用的数学方法是 .
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2). 查看习题详情和答案>>
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x0,y0),则:
|
当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,将(3)代入(4)
得:y0=2x0-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2). 查看习题详情和答案>>
阅读材料:当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1…(1)
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x0,y0),则:
当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,将(3)代入(4)
得:y0=2x0-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是______,其中运用的公式是______.由(3)、(4)得到(5)所用的数学方法是______.
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2).
查看习题详情和答案>>
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x0,y0),则:
|
当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,将(3)代入(4)
得:y0=2x0-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是______,其中运用的公式是______.由(3)、(4)得到(5)所用的数学方法是______.
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2).
阅读材料:当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1…(1)
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x,y),则:
当m的值变化时,顶点横、纵坐标x,y的值也随之变化,将(3)代入(4)
得:y=2x-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是______,其中运用的公式是______.由(3)、(4)得到(5)所用的数学方法是______.
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2).
查看习题详情和答案>>
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x,y),则:

当m的值变化时,顶点横、纵坐标x,y的值也随之变化,将(3)代入(4)
得:y=2x-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是______,其中运用的公式是______.由(3)、(4)得到(5)所用的数学方法是______.
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2).
查看习题详情和答案>>
 阅读理解
阅读理解九年级一班数学学习兴趣小组在解决下列问题中,发现该类问题不仅可以应用“三角形相似”知识解决问题,还可以“建立直角坐标系、应用一次函数”解决问题.
请先阅读下列“建立直角坐标系、应用一次函数”解决问题的方法,然后再应用此方法解决后续问题.
问题:如图(1),直立在点D处的标杆CD长3m,站立在点F处的观察者从点E处看到标杆顶C、旗杆顶A在一条直线上.已知BD=15m,FD=2m,EF=1.6m,求旗杆高AB.
解:建立如图(2)所示的直角坐标系,则线段AE可看作一个一次函数的图象.
由题意可得各点坐标为:点E(0,1.6),C(2,3),B(17,0),且所求的高度就为点A的纵坐标.
设直线AE的函数关系式为y=kx+b.
把E(0,1.6),C(2,3)代入得
|
|

∴y=0.7x+1.6.
∴当x=17时,y=0.7×17+1.6=13.5,即AB=13.5(m).
解决问题
请应用上述方法解决下列问题:
如图(3),河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,BD=9m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.6m,求路灯杆AB的高度. 查看习题详情和答案>>