题目内容
当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1…(1)
得:y=(x-m)2+2m-1…(2)
∴抛物线的顶点坐标为(m,2m-1),设顶点为P(x0,y0),则: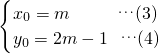
当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,将(3)代入(4)
得:y0=2x0-1.…(5)
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x-1.
解答问题:
①在上述过程中,由(1)到(2)所用的数学方法是______,其中运用的公式是______.由(3)、(4)得到(5)所用的数学方法是______.
②根据阅读材料提供的方法,确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.
③是否存在实数m,使抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0)之间的距离为AB=4,若存在,求出m的值;若不存在,说明理由(提示:|x1-x2|2=(x1+x2)2-4x1x2).
解:(1)配方法;完全平方公式;消元法;
(2)y=x2-2mx+2m2-4m+3=(x-m)2+2m2-4m+2,
∴抛物线的顶点坐标为(m,2m2-4m+2),设顶点为P(x0,y0),则: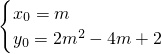 ,
,
当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,
∴y0=2x02-4x0+2,
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x2-4x+2;
(3)不存在.理由如下:
∵抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0),
∴x2-2mx+2m2-4m+3=0的两个根为x1、x2,
∴x1+x2=2m,x1•x2=2m2-4m+3,
∴AB=|x1-x2|= =
=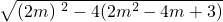 =
=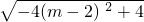 ,
,
∴AB的最大值为2,
∴不存在实数m,使AB=4.
分析:(1)利用配方法把二次函数的一般式配成顶点式,通过消元可得到抛物线的顶点坐标都满足的函数关系;
(2)根据(1)给的方法:先配成y=(x-m)2+2m2-4m+2,得到顶点坐标,然后消去m,得到y与x的关系式;
(3)先根据根与系数的关系得到x1+x2=2m,x1•x2=2m2-4m+3,然后利用AB=|x1-x2|,通过变形得到AB=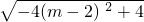 ,即可得到AB的最大值为2,由此得到不存在实数m,使AB=4.
,即可得到AB的最大值为2,由此得到不存在实数m,使AB=4.
点评:本题考查了二次函数综合题:抛物线的顶点式y=a(x-h)2+k(a≠0),则顶点坐标为(h,k);抛物线与x轴两交点的距离.也考查了代数式的变形能力.
(2)y=x2-2mx+2m2-4m+3=(x-m)2+2m2-4m+2,
∴抛物线的顶点坐标为(m,2m2-4m+2),设顶点为P(x0,y0),则:
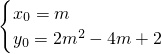 ,
,当m的值变化时,顶点横、纵坐标x0,y0的值也随之变化,
∴y0=2x02-4x0+2,
可见,不论m取任何实数时,抛物线的顶点坐标都满足y=2x2-4x+2;
(3)不存在.理由如下:
∵抛物线y=x2-2mx+2m2-4m+3与x轴两交点A(x1,0)、B(x2,0),
∴x2-2mx+2m2-4m+3=0的两个根为x1、x2,
∴x1+x2=2m,x1•x2=2m2-4m+3,
∴AB=|x1-x2|=
 =
=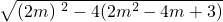 =
=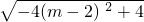 ,
,∴AB的最大值为2,
∴不存在实数m,使AB=4.
分析:(1)利用配方法把二次函数的一般式配成顶点式,通过消元可得到抛物线的顶点坐标都满足的函数关系;
(2)根据(1)给的方法:先配成y=(x-m)2+2m2-4m+2,得到顶点坐标,然后消去m,得到y与x的关系式;
(3)先根据根与系数的关系得到x1+x2=2m,x1•x2=2m2-4m+3,然后利用AB=|x1-x2|,通过变形得到AB=
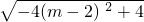 ,即可得到AB的最大值为2,由此得到不存在实数m,使AB=4.
,即可得到AB的最大值为2,由此得到不存在实数m,使AB=4.点评:本题考查了二次函数综合题:抛物线的顶点式y=a(x-h)2+k(a≠0),则顶点坐标为(h,k);抛物线与x轴两交点的距离.也考查了代数式的变形能力.

练习册系列答案
相关题目
 (x,y)为整点,该函数的图象为整点抛物线(例如:y=x2+2x+2).
(x,y)为整点,该函数的图象为整点抛物线(例如:y=x2+2x+2). (2012•南平)在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(m,1)(m>0),将此矩形绕O点逆时针旋转90°,得到矩形OA′B′C′.
(2012•南平)在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(m,1)(m>0),将此矩形绕O点逆时针旋转90°,得到矩形OA′B′C′.