摘要：证明.∵∠ACB=90o.CE⊥AD.∴∠CAD=∠BCF 2分 又∵BF∥AC.∴∠FBC=∠DCA=90o.而AC=BC ∴△FBC≌△DCA ∴FB=CD 4分 又∵D是BC的中点.∴CD=DB 故DB=FB.即△DBF为等腰三角形 6分 又由AC=BC知 ∠CAB=∠CBA BF∥AC知 ∠CAB=∠ABF 故∠CBA=∠ABF (说明:此处学生若从 ∠CBA=∠ABF= 来论证可酌情给分 ) 即AB为等腰三角形DBF的顶角平分线 ∴AB垂直平分DF 8分
网址：http://m.1010jiajiao.com/timu3_id_440253[举报]
如图，在等腰Rt△ABC中，∠ACB=90o，AC=CB，F是AB边上的中点，点D、E分别在AC、BC边上运动，且始终保持AD=CE．连接DE、DF、EF．
（1）求证：△ADF≌△CEF
（2）试证明△DFE是等腰直角三角形.
（1）求证：△ADF≌△CEF
（2）试证明△DFE是等腰直角三角形.
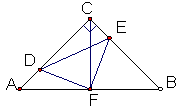
如图，在等腰Rt△ABC中，∠ACB=90o,AC=CB，F是AB边上的中点,点D、E分别在AC、BC边上运动，且始终保持AD=CE．连接DE、DF、EF．
（1）求证：△ADF≌△CEF
（2）试证明△DFE是等腰直角三角形.
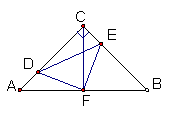
如图，在等腰Rt△ABC中，∠ACB=90o,AC=CB，F是AB边上的中点,点D、E分别在AC、BC边上运动，且始终保持AD=CE．连接DE、DF、EF．
（1）求证：△ADF≌△CEF
（2）试证明△DFE是等腰直角三角形.
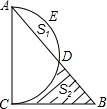如图，以△ABC的边AC为直径的半圆交AB于D，三边长a，b，c能使二次函数
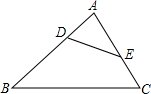如图，D、E两点分别在△ABC的边AB、AC上，DE与BC不平行．