摘要：小明求方程的解时.分别画出了函数y＝x2和的图象.如图.则它们交点A. B的横坐标-和2就是原方程的解. 根据小明的解法. (1)求方程的解的个数, (2)求方程的解的个数.
网址：http://m.1010jiajiao.com/timu3_id_439028[举报]
探索一个问题：
“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（阅读（1）完成后面的问题）
1） ．当已知矩形A的边长分别为6和1时，小亮同学是这样研究的：设所求矩形的两边分别是，
由题意得方程组：
，
消去y化简得：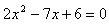
∵△=49-48>0
∴
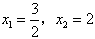∴满足要求的矩形B存在；
2）．如果已知矩形A的边长分别为2和1，请你仿照小亮的方法研究是否存在满足要求的矩形B．
3）．对上述（2）中问题，小明同学从“图形”的角度，利用函数图象给予了解决．小明论证的过程开始是这样的：如果用x、y分别表示矩形的长和宽，那么矩形B满足x+y=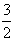
，xy=1．请你按照小明的论证思路完成后面的论证过程．
“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（阅读（1）完成后面的问题）
1） ．当已知矩形A的边长分别为6和1时，小亮同学是这样研究的：设所求矩形的两边分别是，
由题意得方程组：
，消去y化简得：
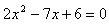
∵△=49-48>0
∴
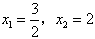∴满足要求的矩形B存在；2）．如果已知矩形A的边长分别为2和1，请你仿照小亮的方法研究是否存在满足要求的矩形B．
3）．对上述（2）中问题，小明同学从“图形”的角度，利用函数图象给予了解决．小明论证的过程开始是这样的：如果用x、y分别表示矩形的长和宽，那么矩形B满足x+y=
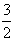，xy=1．请你按照小明的论证思路完成后面的论证过程．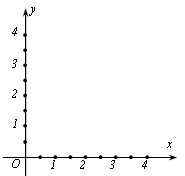 
4）．如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y分别表示矩形B的两边长，请你结合刚才的研究，回答下列问题：
①．这个图象所研究的矩形A的两边长为___ __和__ ___；
②．满足条件的矩形B的两边长为___ __和___ __．
①．这个图象所研究的矩形A的两边长为___ __和__ ___；
②．满足条件的矩形B的两边长为___ __和___ __．
探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”
（1）完成下列空格：
当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的一边是x，则另一边为（
-x），由题意得方程：x（-x）=3，化简得：2x2-7x+6=0
∵b2-4ac=49-48＞0，∴x1=______，x2=______．
∴满足要求的矩形B存在．
小红的做法是：设所求矩形的两边分别是x和y，由题意得方程组：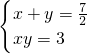
消去y化简后也得到：2x2-7x+6=0，（以下同小明的做法）
（2）如果已知矩形A的边长分别为2和1，请你仿照小明或小红的方法研究是否存在满足要求的矩形B．
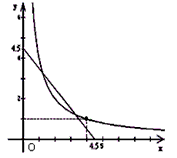
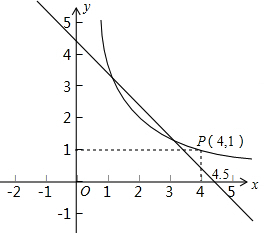
（3）在小红的做法中，我们可以把方程组整理为：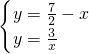
，此时两个方程都可以看成是函数解析式，从而我们可以利用函数图象解决一些问题．如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y分别表示矩形B的两边长，请你结合刚才的研究，回答下列问题：（完成下列空格）
①这个图象所研究的矩形A的面积为______；周长为______．
②满足条件的矩形B的两边长为______和______．
查看习题详情和答案>>
探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”
（1）完成下列空格：
当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的一边是x，则另一边为（
-x），由题意得方程：x（
-x）=3，化简得：2x2-7x+6=0
∵b2-4ac=49-48＞0，∴x1=______，x2=______．
∴满足要求的矩形B存在．
小红的做法是：设所求矩形的两边分别是x和y，由题意得方程组：
消去y化简后也得到：2x2-7x+6=0，（以下同小明的做法）
（2）如果已知矩形A的边长分别为2和1，请你仿照小明或小红的方法研究是否存在满足要求的矩形B．
（3）在小红的做法中，我们可以把方程组整理为：
，此时两个方程都可以看成是函数解析式，从而我们可以利用函数图象解决一些问题．如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y分别表示矩形B的两边长，请你结合刚才的研究，回答下列问题：（完成下列空格）
①这个图象所研究的矩形A的面积为______；周长为______．
②满足条件的矩形B的两边长为______
查看习题详情和答案>>
（1）完成下列空格：
当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的一边是x，则另一边为（
-x），由题意得方程：x（-x）=3，化简得：2x2-7x+6=0∵b2-4ac=49-48＞0，∴x1=______，x2=______．
∴满足要求的矩形B存在．
小红的做法是：设所求矩形的两边分别是x和y，由题意得方程组：
消去y化简后也得到：2x2-7x+6=0，（以下同小明的做法）（2）如果已知矩形A的边长分别为2和1，请你仿照小明或小红的方法研究是否存在满足要求的矩形B．
（3）在小红的做法中，我们可以把方程组整理为：
，此时两个方程都可以看成是函数解析式，从而我们可以利用函数图象解决一些问题．如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y分别表示矩形B的两边长，请你结合刚才的研究，回答下列问题：（完成下列空格）①这个图象所研究的矩形A的面积为______；周长为______．
②满足条件的矩形B的两边长为______
查看习题详情和答案>>
（2012•西城区模拟）探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（1）完成下列空格：
当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的一边是x，则另一边为（
| 7 |
| 2 |
| 7 |
| 2 |
∵b2-4ac=49-48＞0，∴x1=
2
2
，x2=| 3 |
| 2 |
| 3 |
| 2 |
∴满足要求的矩形B存在．
小红的做法是：设所求矩形的两边分别是x和y，由题意得方程组：
|
（2）如果已知矩形A的边长分别为2和1，请你仿照小明或小红的方法研究是否存在满足要求的矩形B．
（3）在小红的做法中，我们可以把方程组整理为：
|
①这个图象所研究的矩形A的面积为
8
8
；周长为18
18
．②满足条件的矩形B的两边长为
9+
| ||
| 4 |
9+
| ||
| 4 |
9-
| ||
| 4 |
9-
| ||
| 4 |
| （1）甲乙两辆汽车在一条公路上匀速行驶，为了确定汽车的位置，我们用数轴O表示这条公路，原点O为零千米路标（如图1），并作如下约定： ①速度v>0，表示汽车向数轴正方向行驶；速度v＜0，表示汽车向数轴负方向行驶；速度v=0，表示汽车静止。 ②汽车位置在数轴上的坐标s>0，表示汽车位于零千米路标的右侧；汽车位置在数轴上的坐标s＜0，表示汽车位于零千米路标的左侧；汽车位置在数轴上的坐标s=0，表示汽车恰好位于零千米路标处，遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数图象的形式画在了同一直角坐标系中，如图2。 | ||||||||||||
 | ||||||||||||
| 请解答下列问题： ①就这两个一次函数图像所反映的两汽车在这条公路上行驶的状况填写如下的表格： | ||||||||||||
| ||||||||||||
| （2）在一次蜡烛燃烧实验中，甲、乙两根蜡烛燃烧时剩余的高度y（cm）与燃烧时间x（分钟）的关系如下图所示，根据图像提供的信息解答下列问题： | ||||||||||||
 | ||||||||||||
| ①指出两根蜡烛燃烧前的高度； ②分别求出甲、乙两根蜡烛燃烧时y与x之间的函数关系式； ③x为何值时，甲、乙两根蜡烛在燃烧过程中的高度相等。 |