摘要：已知锐角△ABC中.AB=15.BC=14.S△ABC=84.则tgC= .
网址：http://m.1010jiajiao.com/timu3_id_438355[举报]
（2013•奉贤区一模）通过学习锐角三角比，我们知道在直角三角形中，一个锐角的大小与两条边长的比值是一一对应的，因此，两条边长的比值与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做底角的邻对（can），如图（1）在△ABC中，AB=AC，底角B的邻对记作canB，这时canB=
=
，容易知道一个角的大小与这个角的邻对值也是一一对应的．根据上述角的邻对的定义，解下列问题：
（1）can30°=
；
（2）如图（2），已知在△ABC中，AB=AC，canB=
，S△ABC=24，求△ABC的周长．
查看习题详情和答案>>
| 底边 |
| 腰 |
| BC |
| AB |
（1）can30°=
| 3 |
| 3 |
（2）如图（2），已知在△ABC中，AB=AC，canB=
| 8 |
| 5 |
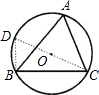
阅读材料，解答问题：命题：如图，在锐角△ABC中，BC=a，CA=b，AB=c，△ABC的外接圆半径为R，则
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
证明：连接CO并延长交⊙O于点D，连接DB，则∠D=∠A．
因为CD是⊙O的直径，所以∠DBC=90°，
在Rt△DBC中，sin∠D=
| BC |
| DC |
| a |
| 2R |
所以sinA=
| a |
| 2R |
| a |
| sinA |
同理：
| b |
| sinB |
| c |
| sinC |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
请阅读前面所给的命题和证明后，完成下面（1）（2）两题：
（1）前面阅读材料中省略了“
| b |
| sinB |
| c |
| sinC |
| b |
| sinB |
（2）直接运用阅读材料中命题的结论解题，已知锐角△ABC中，BC=
| 3 |
| 2 |
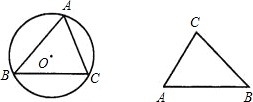查看习题详情和答案>>
