题目内容
（2013•奉贤区一模）通过学习锐角三角比，我们知道在直角三角形中，一个锐角的大小与两条边长的比值是一一对应的，因此，两条边长的比值与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做底角的邻对（can），如图（1）在△ABC中，AB=AC，底角B的邻对记作canB，这时canB=
=
，容易知道一个角的大小与这个角的邻对值也是一一对应的．根据上述角的邻对的定义，解下列问题：
（1）can30°=
；
（2）如图（2），已知在△ABC中，AB=AC，canB=
，S△ABC=24，求△ABC的周长．
| 底边 |
| 腰 |
| BC |
| AB |
（1）can30°=
| 3 |
| 3 |
（2）如图（2），已知在△ABC中，AB=AC，canB=
| 8 |
| 5 |
分析：（1）过点A作AD⊥BC于点D，根据∠B=30°，可得出BD=
AB，结合等腰三角形的性质可得出BC=
AB，继而得出canB；
（2）过点A作AE⊥BC于点E，根据canB=
，设BC=8x，AB=5x，再由S△ABC=24，可得出x的值，继而求出周长．
| ||
| 2 |
| 3 |
（2）过点A作AE⊥BC于点E，根据canB=
| 8 |
| 5 |
解答：解：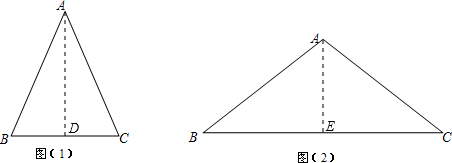
（1）过点A作AD⊥BC于点D，
∵∠B=30°，
∴cos∠B=
=
，
∴BD=
AB，
∵△ABC是等腰三角形，
∴BC=2BD=
AB，
故can30°=
=
；
（2）过点A作AE⊥BC于点E，
∵canB=
，则可设BC=8x，AB=5x，
∴AE=
=3x，
∵S△ABC=24，
∴
BC×AE=12x2=24，
解得：x=
，
故AB=AC=5
，BC=8
，
从而可得△ABC的周长为18
．
（1）过点A作AD⊥BC于点D，
∵∠B=30°，
∴cos∠B=
| BD |
| AB |
| ||
| 2 |
∴BD=
| ||
| 2 |
∵△ABC是等腰三角形，
∴BC=2BD=
| 3 |
故can30°=
| BC |
| AB |
| 3 |
（2）过点A作AE⊥BC于点E，
∵canB=
| 8 |
| 5 |
∴AE=
| AB2-BE2 |
∵S△ABC=24，
∴
| 1 |
| 2 |
解得：x=
| 2 |
故AB=AC=5
| 2 |
| 2 |
从而可得△ABC的周长为18
| 2 |
点评：本题考查了解直角三角形及勾股定理的知识，解答本题的关键是熟练掌握等腰三角形的性质，表示出各个边的长度．
练习册系列答案
口算题天天练系列答案
相关题目
（2013•奉贤区一模）在Rt△ABC中，∠C=90°，AB=5，BC=3，点D、E分别在BC、AC上，且BD=CE，设点C关于DE的对称点为F，若DF∥AB，则BD的长为