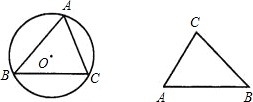题目内容

已知锐角△ABC中，AC=15，AB=13，高AD=12，则边BC的长为
14
14
．
分析：在锐角三角形ABC中，根据勾股定理求得BD，CD，根据图形即可得出BC=BD+CD．
解答：解：如图，

在Rt△ABD中AB=13，AD=12，
由勾股定理得：BD2=AB2-AD2=132-122=25，
则BD=5，
在Rt△ABD中AC=15，AD=12，
由勾股定理得：CD2=AC2-AD2=152-122=81，
则CD=9，
故BC的长为BD+DC=9+5=14，
故答案为：14．
点评：本题考查了勾股定理的知识，难度一般，解答本题的关键是把三角形斜边转化到直角三角形中用勾股定理解答．
练习册系列答案
相关题目
精英家教网阅读材料，解答问题：
命题：如图，在锐角△ABC中，BC=a，CA=b，AB=c，△ABC的外接圆半径为R，则
a
sinA
=
b
sinB
=
c
sinC
=2R．
证明：连接CO并延长交⊙O于点D，连接DB，则∠D=∠A．
因为CD是⊙O的直径，所以∠DBC=90°，
在Rt△DBC中，sin∠D=
BC
DC
=
a
2R
，
所以sinA=
a
2R
，即
a
sinA
=2R，
同理：
b
sinB
=2R，
c
sinC
=2R，
a
sinA
=
b
sinB
=
c
sinC
=2R，
请阅读前面所给的命题和证明后，完成下面（1）（2）两题：
（1）前面阅读材料中省略了“
b
sinB
=2R，
c
sinC
=2R”的证明过程，请你把“
b
sinB
=2R”的证明过程补写出来．
（2）直接运用阅读材料中命题的结论解题，已知锐角△ABC中，BC=
3
，CA=
2
，∠A=60°，求△ABC的外接圆半径R及∠C．
精英家教网
已知锐角△ABC中，sinA=
2
2
，cotB=
3
3
，则∠C=
 
．
已知锐角△ABC中，AD⊥BC于D，∠B=45°，DC=1，且S△ABC=3，则AB=
 
．
已知锐角△ABC中，BC=30，BC边上的高h=20
（1）如图1，△ABC的内接正方形的两顶点在BC上，另两顶点分别在AC，AB上，求这个正方形的面积；
（2）如图2，点M在线段AB上（不同于A，B），MN∥BC交AC于N，以MN为边向下作矩形MNPQ，且满足MQ=2MN，设MN=x，矩形MNPQ和△ABC的公共部分的面积为y，直接写出y与x的函数关系式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网