摘要：26．如图13-1.操作:把正方形CGEF的对角线 CE放在正方形ABCD的边BC的延长线上. 取线段AE的中点M. 探究:线段MD.MF的关系.并加以证明. 说明:(1)如果你经历反复探索.没有找到解决问题 的方法.请你把探索过程中的某种思路写出来(要求 至少写3步),的过程之后. 可以从下列①.②.③中选取一个补充或更换已知条件. 完成你的证明. 注意:选取①完成证明得10分,选取②完成证明得 7分,选取③完成证明得5分. ① DM的延长线交CE于点N.且AD＝NE, ② 将正方形CGEF绕点C逆时针旋转45°. 其他条件不变,③在②的条件下且CF＝2AD. 附加题:将正方形CGEF绕点C旋转任意角度后 .其他条件不变.探究:线段MD. MF的关系.并加以证明.
网址：http://m.1010jiajiao.com/timu3_id_437820[举报]
如图，是一个“有理数转换器”（箭头是指数进入转换器的路径，方框是对进入的数进行转换的转换器）
（1）当小明输入-3、4这2个数时，这四次输出的结果分别是
；1
；1；
（2）有一次，小明在操作的时候，输出的结果是3，你判断一下，小明可能输入的数是什么数？（最多写4个数即可）
查看习题详情和答案>>
（1）当小明输入-3、4这2个数时，这四次输出的结果分别是
| 1 |
| 3 |
| 1 |
| 3 |
（2）有一次，小明在操作的时候，输出的结果是3，你判断一下，小明可能输入的数是什么数？（最多写4个数即可）
（2012•北京）操作与探究：
（1）对数轴上的点P进行如下操作：先把点P表示的数乘以
，再把所得数对应的点向右平移1个单位，得到点P的对应点P′．
点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′．如图1，若点A表示的数是-3，则点A′表示的数是
．
（2）如图2，在平面直角坐标系xOy中，对正方形ABCD及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a，将得到的点先向右平移m个单位，再向上平移n个单位（m＞0，n＞0），得到正方形A′B′C′D′及其内部的点，其中点A，B的对应点分别为A′，B′．已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合，求点F的坐标．
查看习题详情和答案>>
（1）对数轴上的点P进行如下操作：先把点P表示的数乘以
| 1 |
| 3 |
点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′．如图1，若点A表示的数是-3，则点A′表示的数是
0
0
；若点B′表示的数是2，则点B表示的数是3
3
；已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合，则点E表示的数是| 3 |
| 2 |
| 3 |
| 2 |
（2）如图2，在平面直角坐标系xOy中，对正方形ABCD及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a，将得到的点先向右平移m个单位，再向上平移n个单位（m＞0，n＞0），得到正方形A′B′C′D′及其内部的点，其中点A，B的对应点分别为A′，B′．已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合，求点F的坐标．
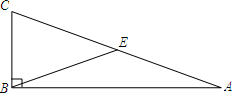如图，△ABC中，∠ABC=90°，E为AC的中点．操作：过点C作BE的垂线，过点A作BE的平行线，两直线相交于点D，在AD的延长线上截取DF=BE．连接EF、BD．
（1）试判断EF与BD之间具有怎样的关系？并证明你所得的结论．
（2）如果AF=13，CD=6，求AC的长． 查看习题详情和答案>>
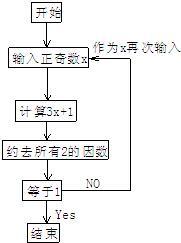20、利用计算器，按如图流程图操作：