题目内容
(2012•北京)操作与探究:
(1)对数轴上的点P进行如下操作:先把点P表示的数乘以
,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.
点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是-3,则点A′表示的数是
.

(2)如图2,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.

(1)对数轴上的点P进行如下操作:先把点P表示的数乘以
| 1 |
| 3 |
点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是-3,则点A′表示的数是
0
0
;若点B′表示的数是2,则点B表示的数是3
3
;已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是| 3 |
| 2 |
| 3 |
| 2 |

(2)如图2,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.

分析:(1)根据题目规定,以及数轴上的数向右平移用加计算即可求出点A′,设点B表示的数为a,根据题意列出方程求解即可得到点B表示的数,设点E表示的数为b,根据题意列出方程计算即可得解;
(2)先根据向上平移横坐标不变,纵坐标加,向右平移横坐标加,纵坐标不变求出平移规律,然后设点F的坐标为(x,y),根据平移规律列出方程组求解即可.
(2)先根据向上平移横坐标不变,纵坐标加,向右平移横坐标加,纵坐标不变求出平移规律,然后设点F的坐标为(x,y),根据平移规律列出方程组求解即可.
解答:解:(1)点A′:-3×
+1=-1+1=0,
设点B表示的数为a,则
a+1=2,
解得a=3,
设点E表示的数为b,则
b+1=b,
解得b=
;
故答案为:0,3,
;
(2)根据题意得,
,
解得
,
设点F的坐标为(x,y),
∵对应点F′与点F重合,
∴
x+
=x,
y+2=y,
解得x=1,y=4,
所以,点F的坐标为(1,4).
| 1 |
| 3 |
设点B表示的数为a,则
| 1 |
| 3 |
解得a=3,
设点E表示的数为b,则
| 1 |
| 3 |
解得b=
| 3 |
| 2 |
故答案为:0,3,
| 3 |
| 2 |
(2)根据题意得,
|
解得
|
设点F的坐标为(x,y),
∵对应点F′与点F重合,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得x=1,y=4,
所以,点F的坐标为(1,4).
点评:本题考查了坐标与图形的变化,数轴上点右边的总比左边的大的性质,读懂题目信息是解题的关键.

练习册系列答案
相关题目
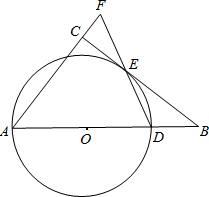 (2012•北京二模)已知:如图,Rt△ABC中,点D在斜边AB上,以AD为直径的⊙O与BC相切于点E,连接DE
(2012•北京二模)已知:如图,Rt△ABC中,点D在斜边AB上,以AD为直径的⊙O与BC相切于点E,连接DE
 (2012•北京)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=
(2012•北京)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=