摘要: 解:(1)证法一:连结CD. ---1分 ∵BC为⊙O的直径 ∴CD⊥AB ---3分 ∵AC=BC ∴AD=BD. ---5分 证法二:连结CD. ---1分 ∵BC为⊙O的直径 ∴∠ADC=∠BDC=90° ---3分 ∵AC=BC.CD=CD ∴△ACD≌△BCD ---4分 ∴AD=BD ---5分 (2)证法一:连结OD. ---6分 ∵AD=BD.OB=OC ∴OD∥AC ---8分 ∵DE⊥AC ∴DF⊥OD ---9分 ∴DF是⊙O的切线. ---10分 证法二:连结OD. ---6分 ∵OB=OD ∴∠BDO=∠B ∵∠B=∠A ∴∠BDO=∠A ---8分 ∵∠A+∠ADE=90° ∴∠BDO+∠ADE=90° ∴∠ODF=90° ---9分 ∴DF是⊙O的切线. ---10分
网址:http://m.1010jiajiao.com/timu3_id_437758[举报]
(2013•东城区一模)在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-9与x轴交于A,B两点(点A在点B的左侧,且OA<OB),与y轴的交点坐标为(0,-5).点M是线段AB上的任意一点,过点M(a,0)作直线MC⊥x轴,交抛物线于点C,记点C关于抛物线对称轴的对称点为D(C,D不重合),点P是线段MC上一点,连结CD,BD,PD.
(1)求此抛物线的解析式;
(2)当a=1时,问点P在什么位置时,能使得PD⊥BD;
(3)若点P满足MP=
MC,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
查看习题详情和答案>>
(1)求此抛物线的解析式;
(2)当a=1时,问点P在什么位置时,能使得PD⊥BD;
(3)若点P满足MP=
| 1 | 4 |

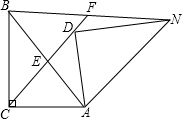 (2013•怀柔区一模)如图,△ABC中,∠ACB=90°,AD=AC,AB=AN,连结CD、BN,CD的延长线交BN于点F.
(2013•怀柔区一模)如图,△ABC中,∠ACB=90°,AD=AC,AB=AN,连结CD、BN,CD的延长线交BN于点F.(1)当∠ADN等于多少度时,∠ACE=∠EBF,并说明理由;
(2)在(1)的条件下,设∠ABC=α,∠CAD=β,试探索α、β满足什么关系时,△ACE≌△FBE,并说明理由.
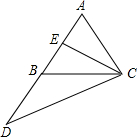 (2013•大兴区一模)已知:如图,在△ABC中,AB=AC,延长AB到点D,使BD=AB,取AB的中点E,连结CD和CE.
(2013•大兴区一模)已知:如图,在△ABC中,AB=AC,延长AB到点D,使BD=AB,取AB的中点E,连结CD和CE.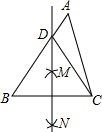 (2013•德惠市一模)如图,△ABC中,AB=6,AC=4,分别以点B和点C为圆心,以大于BC一半的长为半径画弧,两弧相交于点M和N,作直线MN.直线MN交AB于点D,连结CD,则△ADC的周长为
(2013•德惠市一模)如图,△ABC中,AB=6,AC=4,分别以点B和点C为圆心,以大于BC一半的长为半径画弧,两弧相交于点M和N,作直线MN.直线MN交AB于点D,连结CD,则△ADC的周长为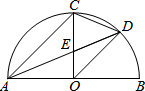 (2014•宁波一模)如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④CD2=CE•CO.其中正确结论的序号是( )
(2014•宁波一模)如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④CD2=CE•CO.其中正确结论的序号是( )